다 변수 데이터의 특이점을 감지하면 종종 데이터 전처리의 문제 중 하나 일 수 있습니다. 단계.특이점을 감지하는 다양한 거리 메트릭, 점수 및 기술이 있습니다.유클리드 거리는 중심점까지의 거리를 기반으로 한 이상을 식별하는 가장 알려진 거리 메트릭 중 하나입니다.또한 단일 숫자 변수에 대한 이상을 정의하는 z 점수가 있습니다.경우에 따라 클러스터링 알고리즘도 선호 될 수 있습니다.이러한 모든 방법은 다른 관점에서 이상 치를 고려합니다.하나의 방법을 기반으로 한 이상이 다른 방법으로 발견되지 않을 수 있습니다.따라서 이러한 방법 및 메트릭은 변수의 배포를 고려하여 선택해야합니다.그러나 이것은 다른 메트릭의 요구도 가져옵니다.이 기사에서는 MahalAnobis 거리라는 거리 메트릭을 다 변수 할 수있는 데이터의 특이점을 감지하기 위해 논의 할 것입니다.

Mahalanobis 거리

Mahalanobis 거리 (MD)는 점과 분포 사이의 거리를 찾는 유효 거리 측정 기준입니다 (또한보십시오짐마자데이터 포인트와 중심 간의 거리를 찾기 위해 변수의 공분산 행렬을 사용하기 때문에 다 변수 데이터에 매우 효과적으로 작동합니다 (공식 1 참조).즉, EUCLIDEAN 거리와 달리 데이터 포인트의 배포 패턴을 기반으로 한 이상을 감지 함을 의미합니다.그 차이를 이해하려면 그림 1을 참조하십시오.

그림 1에서 볼 수 있듯이 데이터 포인트는 특정 방향으로 흩어져 있습니다.유클리드의 거리는 그러한 분포의 이상 치명적인 지점을 할당 할 수 있지만 Mahalanobis 거리가 계속 유지 될 수 있습니다.이것은 그림 2에서 본 비선형 관계에도 동일합니다.

이 차이의 주된 이유는 공분산식이 변수가 어떻게 변화 하는지를 나타내기 때문에 공분산 행렬입니다.N 차원 공간의 중앙과 포인트 사이의 거리를 계산하는 동안 공분산을 사용하면 변화에 따라 진정한 임계 값 테두리를 찾는 기능이 있습니다.화학식 1에 도시 된 MD의 거리 공식으로부터 알 수있는 바와 같이, 공분산 매트릭스는 C로서 C이고 그것의 부정적인 제 1 능력이 취해졌다.벡터 XPI는 n 차원 공간에서 관측 좌표를 나타냅니다.예를 들어 세 가지 변수, 첫 번째 행이있는 데이터 세트가있는 경우 다음과 같이 두 번째 행을 나타낼 수 있습니다.XP1 : [13,15,23] 및 XP2 : [12,14,15]…에그러나 이상 치를 식별하는 동안, 각 포인트 사이의 거리를 찾는 대신 중심과 각 관찰 사이의 거리가 발견되어야합니다.중심점은 각 변수의 평균값을 취하여 얻을 수 있습니다.

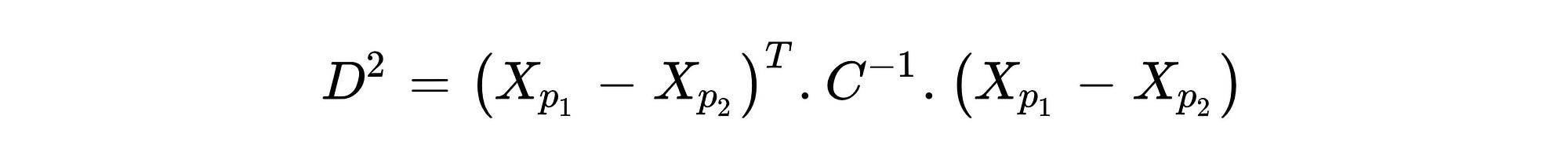
참고 : 그림 1과 2에 주어진 예제 데이터와 달리 변수가 원면에 대부분 흩어지면 유클리드 거리가 더 적합 할 수 있습니다.

파이썬과 Mahalanobis 거리

예, 파이썬을 사용하여 Mahalanobis 거리를 찾을 시간입니다.파이썬 대신 r에 관심이 있으시면 다른 기사를 살펴볼 수 있습니다.

‘scipy’라이브러리에서 Mahalanobis 거리가 있습니다.이 메서드에 액세스 할 수 있습니다scipy.spatial.distance.mahalanobis.또한 세부 사항을 볼 수 있습니다여기…에이 방법을 사용하는 대신, 다음 단계에서는 수식 1에서 주어진 공식을 사용하여 Mahalanobis 거리를 계산하는 자체 방법을 작성하게 될 것입니다.

“AirQuality”라는 데이터 세트를 사용하고 변수 “오존”및 “TEMP”를 사용하여 오위 이상을 감지합니다.이 데이터 세트를 다운로드 할 수 있습니다여기또는 데이터 세트를 사용하십시오.

첫째, 필요한 라이브러리와 데이터 세트를 가져와야합니다.데이터 세트를 계산을 준비하려면 “오존”및 “온도”변수 만 선택되어야합니다.게다가, 아무런 오류가 있지 않아야합니다.또한 Pandas 데이터 프레임을 사용하는 대신 numpy 배열을 사용하는 것을 선호합니다.그래서 내가이를 숫자 배열로 변환했습니다.

두 번째 단계에서는 센터와 포인트 사이의 거리를 계산하기 위해 필요한 값을 얻어야합니다.따라서 “오존”과 “온도”변수 사이의 중심점과 공분산 매트릭스입니다.

세 번째 단계의 경우 데이터 세트의 중심점과 각 관측 (포인트) 사이의 거리를 찾을 준비가되었습니다.우리는 또한 Chi-square 배포에서 컷오프 값을 찾아야합니다.Chi-square가 컷오프 값을 찾는 데 사용되는 이유는 Mahalanobis 거리가 제곱 된 (d²)로 거리를 반환합니다.또한 0.95 (2 꼬리) 외부의 포인트가 이상으로 간주되므로 컷오프를 찾는 동안 컷오프를 찾아야합니다.짧은 양은 컷오프 값이 적습니다.우리는 또한 Chi-square에 대한 자유 값이 필요하며 데이터 세트의 변수 수와 동일합니다.

마지막으로, 우리는 [24, 35, 67, 81]의 인덱스에 4 가지 이상의 특이점이 있습니다.이제이 과정을 더 분명하게 이해하고 계획을 세우십시오.

그리고 여기서 우리는 그림 3에서 볼 수 있듯이, 포인트는 아웃리어로 탐지 된 타원 밖에서 머물러 있습니다.이 ellipse는 MD에 따라 아웃 리어 값을 래핑하는 영역을 나타냅니다.

다음은 무엇입니까?

이 기사에서는 Mahalanobis 거리와 유클리드 거리와의 차이가 논의되었습니다.우리는 또한 파이썬에서 Mahalanobis 거리 공식을 처음부터 적용했습니다.이전에 언급했듯이 데이터가 N 차원 공간에 흩어져있는 방법을 기반으로 거리 측정 항목을 선택하는 것이 중요합니다.다른 거리 메트릭을 살펴볼 수도 있습니다.요리 거리…에

질문이 있으시면 언제든지 코멘트를 남겨주세요.

사용을 따라 이상을 감지하는 방법에 관심이있는 경우 다른 기사를 확인할 수 있습니다.R.의 Mahalanobis 거리…에