일반적으로 코딩과 일상 생활에서 더 많은 경험을 쌓을 때, 저에게 눈에 띄는 것 중 하나는 해결해야 할 문제가있을 때마다 매우 직관적 인 해결책이 있다는 것입니다.때로는이 솔루션이 효율적이고 때로는 매우 차선책입니다.이것은 알고리즘에서 특히 두드러집니다. 알고리즘은 종종 실제 문제의 개념화이기 때문에 알고리즘을 통해 문제의 필수 요소가 유지되어 문제를 직접 해결할 수 있습니다.

가장 큰티제 생각에는 행렬의 직사각형이 그러한 문제 중 하나입니다.다음은 문제에 대한 간략한 설명입니다.

문제

빨간색과 파란색 점으로 된 보드가 있는데 파란색 점으로 형성된 가장 큰 직사각형을 찾고 싶습니다.

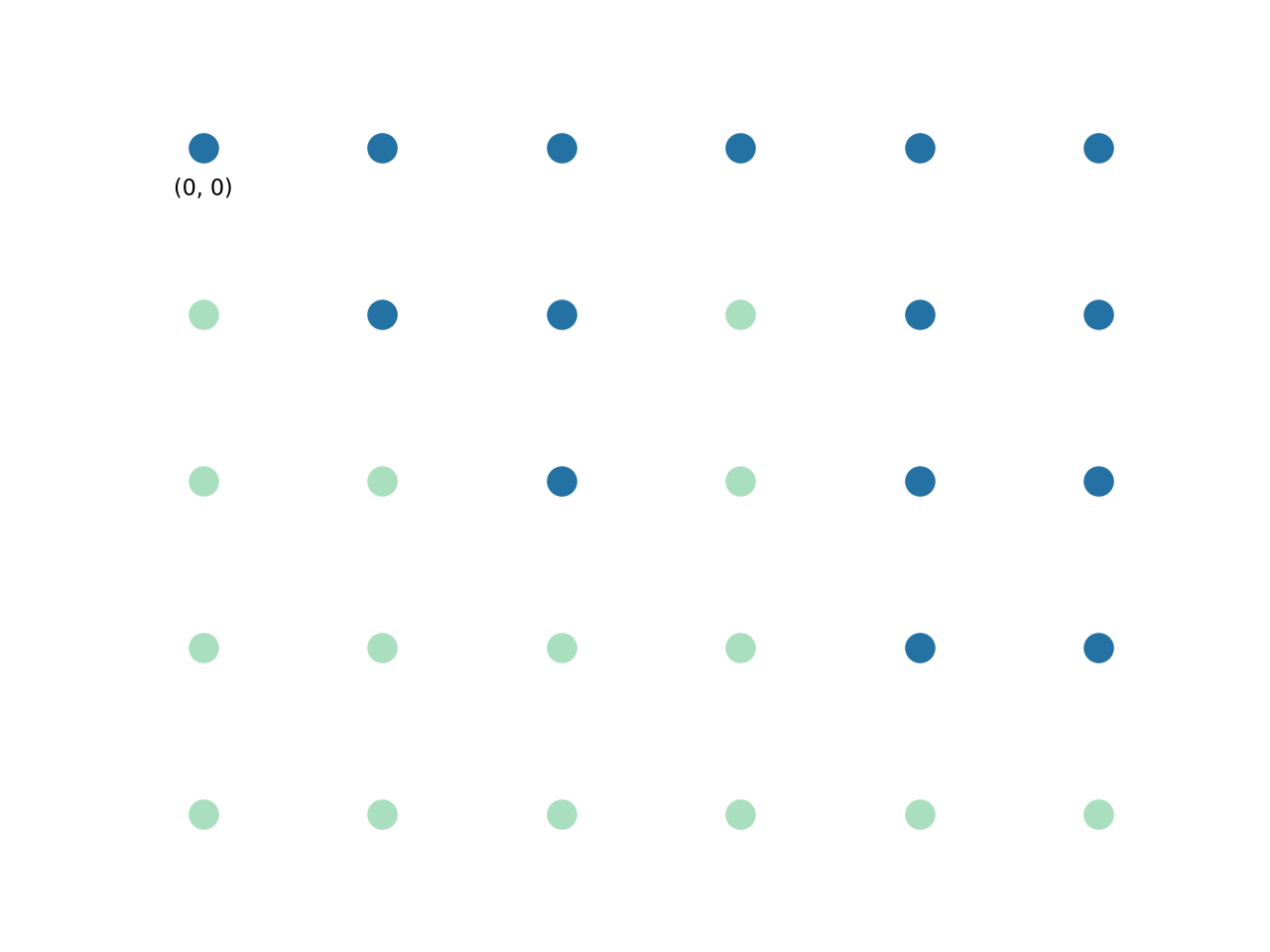
이 예에서는 파란색 점으로 구성된 가장 큰 직사각형의 크기가 8이라는 것을 쉽게 알 수 있습니다.

하지만이를 알고리즘 방식으로 수행하는 방법을 알아 봅시다.

솔루션 # 1

간단하게하는 방법

이 문제를 처음으로 시도했을 때 나는 스스로 생각했습니다.

글쎄요, 아마도 행렬의 모든 점을 반복해야 할 것 같습니다. 그리고 각 점에서 그 점을 포함하는 가장 큰 직사각형을 찾아야합니다.이 사각형을 이미 찾은 사각형의 크기와 비교하겠습니다.새 것이 더 크면 유지하고 그렇지 않으면 다음 지점으로 이동합니다.

훌륭하게 들리지만 문제가 있습니다.특정 점을 포함하는 가장 큰 직사각형을 어떻게 찾습니까?이 문제를 해결하는 데 도움이 될만한 것은 없습니다.

현재 지점이 왼쪽 상단 모서리 인 가장 큰 직사각형을 찾으려면 어떻게해야합니까?나는 이것이 더 관리하기 쉬운 문제라고 생각합니다.

이를 파악하기 위해 현재 지점의 오른쪽에있는 각 지점을 반복하고 각 지점에서 파란색 점의 최대 높이를 찾습니다. 현재 지점의 높이보다 작 으면현재 포인트 높이를 새 높이로 업데이트하고 새 사각형의 크기를 찾습니다. 더 큰 사각형이면 최대 크기를 업데이트합니다.

이 절차를 예제에 적용 해 보겠습니다.

내가 (1, 0) 지점까지 반복했다고 가정합니다.

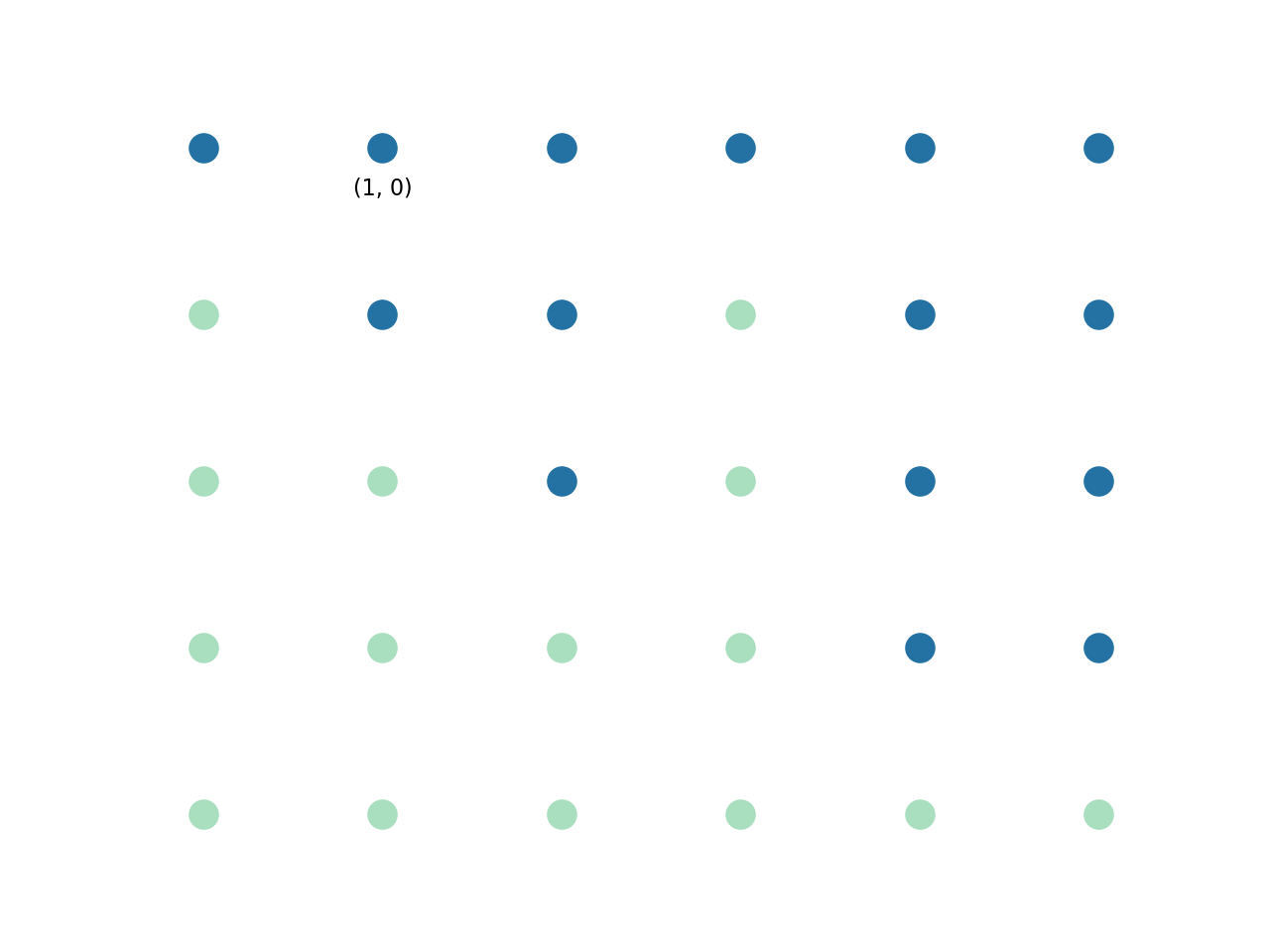
내 현재 포인트의 높이는 2이며,이 정보가 주어지면 오른쪽 상단 모서리가 (1, 0) 인 가장 큰 직사각형 인 2입니다.

(1, 0) : 높이 = 2, max_rectangle = 2.

오른쪽의 모든 지점을 반복합니다.

점 (2, 0)의 높이는 3이지만 시작점보다 크므로 높이는 여전히 2입니다. 그러나 이제 우리는 크기가 2 * 2 = 4 인 직사각형을 가질 수 있음을 알고 있습니다.

(2, 0) : 높이 = 2, max_rectangle = 4

Point (3, 0)의 높이는 1이고 현재 높이보다 작으므로 현재 높이를 1로 업데이트하면 만들 수있는 사각형은 1 * 3 = 3이지만 현재 최대 값은 4이므로 무시합니다.그것:

(3, 0) : 높이 = 1, max_rectangle = 4

나머지 포인트에 대해 동일한 프로세스를 수행합니다.

(4, 0) : 높이 = 1, max_rectangle = 4

(5, 0) : 높이 = 1, max_rectangle = 5

오른쪽 상단 모서리가 (1, 0)이고 크기가 5 인 가장 큰 직사각형을 찾습니다.

이것을 코드에 넣어 보겠습니다.

def find_max001 (행렬) :

너비 = len (matrix [0])
높이 = len (행렬)

# a 지점에서 최대 너비와 최대 높이
# 암기 및 동적 프로그래밍 사용
max_matrix = [[행렬에있는 행에 대해 없음]]
def get_max (i, j) :
i & gt; = 너비 인 경우 :
0, 0 반환
elif j & gt; = 높이 :
0, 0 반환
elif max_matrix [j] [i]가 None이 아닙니다.
max_matrix [j] [i] 반환
elif 행렬 [j] [i] == 0 :
max_matrix [j] [i] = (0, 0)
max_matrix [j] [i] 반환

max_down = get_max (i, j + 1)
max_right = get_max (i + 1, j)

max_matrix [j] [i] = (최대 _ 오른쪽 [0] + 1,
max_down [1] + 1)
max_matrix [j] [i] 반환

max_rect = 0
i 범위 (너비) :
범위 (높이)에있는 j의 경우 :
rect = get_max (i, j)
cur_max = rect [1]
k 범위 (1, rect [0])의 경우 :
cur_max = min (cur_max, get_max (i + k, j) [1])

max_rect = max (max_rect, cur_max * rect [0])

max_rect 반환
def problem003 (솔버) :

m001 = [
[1, 1, 1, 1, 1, 1],
[0, 1, 1, 0, 1, 1],
[0, 0, 1, 0, 1, 1],
[0, 0, 0, 0, 1, 1],
[0, 0, 0, 0, 0, 0]
]

res1 = 솔버 (m001)
print (f'res1 : {res1} ')
def test003 () :
솔버 = find_max001
problem003 (솔버)
test003 ()
# res1 : 8

Performance of Solution #1

알고리즘의 복잡성은 무엇입니까?

각 지점을 반복하기 때문에 복잡성은 적어도 w * h입니다.운 좋게도 우리는 메모 화 및 동적 프로그래밍 기술을 사용하여 각 지점에서 높이를 찾을 수 있으므로 복잡성을 추가하지 않습니다.

각 지점에서 행렬의 너비를 반복하여 해당 지점에서 가장 큰 직사각형을 찾습니다. 이것은 복잡성을 w * h * w로 느리게합니다.

따라서 복잡성은 다음과 같습니다. O (w² * h)

또한 맵을 사용하여 각 지점의 너비와 높이를 저장하기 때문에 :

메모리 사용량은 O (w * h)입니다.

솔루션 # 2

알고리즘을 개선하는 방법은 무엇입니까?

복잡도에서 w² 항을 줄이는 방법이 있습니까?

밝혀졌습니다.

예를 다시 살펴 보겠습니다.

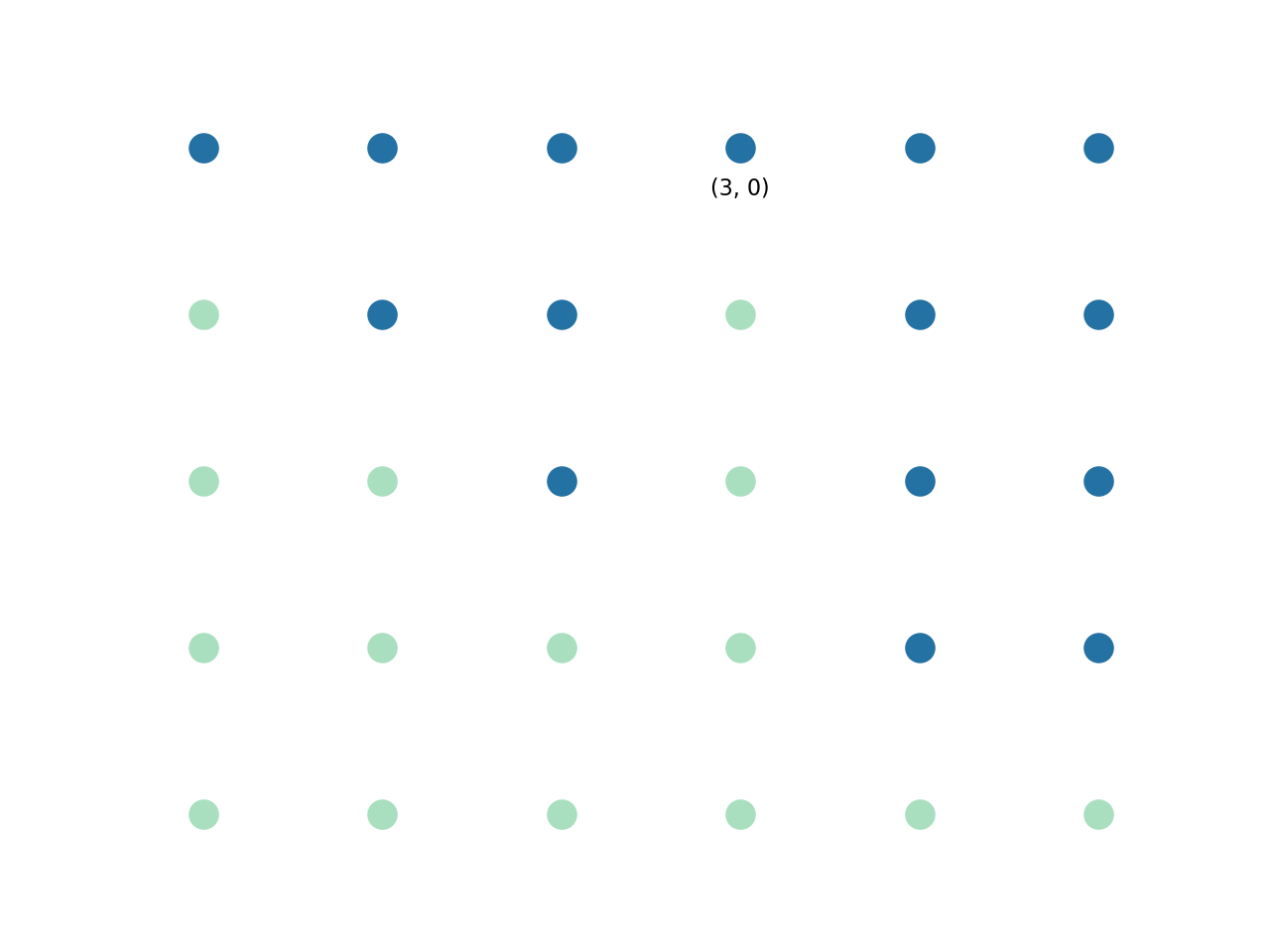
이제 첫 번째 행을 반복한다고 가정합니다.

(0, 0), (1, 0), (2, 0)에서 높이는 1, 2, 3으로 계속 증가합니다. 목록을 유지합니다.

[(0, 0 : 1), (1, 0 : 2), (2, 0 : 3)]

(3, 0) 위치에서 높이가 1로 떨어집니다.이 새로운 정보는 우리에게 무엇을 알려 줍니까?

사실 꽤 그렇습니다.이 정보가 주어지면 높이가 3 인 위치 (2, 0)에 왼쪽 상단 모서리가있는 직사각형은 최대 크기가 3 만 될 수 있습니다.

또한 높이가 2 인 위치 (1, 0)에 왼쪽 상단 모서리가있는 직사각형은 최대 크기가 4 만 될 수 있다고 확신 할 수 있습니다.

두 점을 처리 한 후 영구적으로 제거 할 수 있지만 (1, 0) (참고, (3, 0)이 아님)에 높이 1로 새 점을 추가해야합니다.

[(0, 0 : 1), (1, 0 : 1)]

기본적으로 우리가하는 일은 (2, 0)과 (1, 0)의 높이를 (3, 0)의 높이와 같게 트리밍하는 것입니다.

이 길을 따라 줄 끝까지 이동하면 더 이상 높이가 떨어지지 않습니다.

[(0, 0 : 1), (1, 0 : 1), (5, 0 : 4), (4, 0 : 4)]

그런 다음 나머지 행을 처리 할 수 있습니다.

(5, 0) max_rectangle = 4

(4, 0) max_rectangle = 4 * 2 = 8

(1, 0) max_rectangle = 1 * 5 = 5

(0, 0) max_rectangle = 1 * 6 = 6

따라서 첫 번째 행을 처리 한 후의 max_rectangle은 8이고 6 포인트 만 반복했습니다!이것은 알고리즘의 복잡성이 이제 w * h라는 것을 의미합니다!

다음은 코드의 알고리즘입니다.

컬렉션에서 가져 오기 deque

def find_max002 (매트릭스) :

너비 = len (matrix [0])
높이 = len (행렬)

# 최대 수심
max_matrix = [[행렬에있는 행에 대해 없음]]

def get_max (i, j) :
i & gt; = 너비 인 경우 :
0, 0 반환
elif j & gt; = 높이 :
0, 0 반환
elif max_matrix [j] [i]가 None이 아닙니다.
max_matrix [j] [i] 반환
elif 행렬 [j] [i] == 0 :
max_matrix [j] [i] = (0, 0)
max_matrix [j] [i] 반환

max_down = get_max (i, j + 1)
max_right = get_max (i + 1, j)

max_matrix [j] [i] = (최대 _ 오른쪽 [0] + 1, 최대 _ 아래 [1] + 1)
max_matrix [j] [i] 반환

def get_rect (stack, j) :
cur_idx = stack.pop ()
cur_max = cur_idx [1] * (j-cur_idx [0])
print (f "cur_max at {cur_idx [0]} : {cur_max}")
cur_max 반환

max_rect = 0
i 범위 (너비) :

# 스택으로 알고리즘 구현
스택 = deque ()
stack.append ((-1, 0))
범위 (높이)에있는 j의 경우 :
rect = get_max (i, j)
cur_width = rect [0]
cur_idx = j
스택 [-1] [1] & gt;cur_width :
cur_idx = 스택 [-1] [0]
max_rect = max (max_rect,
get_rect (스택, j))
stack.append ((cur_idx, cur_width))

동안 len (stack) & gt;1:
max_rect = max (max_rect, get_rect (stack, height))

max_rect 반환def test004 () :

솔버 = find_max002

problem003 (솔버)
test004 ()
# res1 : 8

(3, 0)에 도달 한 후 포인트 (2, 0) 및 (1, 0) 제거를 구현하기 위해 스택 데이터 구조를 사용하여 포인트를 효율적으로 푸시하고 팝합니다.

솔루션 # 2의 복잡성

앞서 언급했듯이 솔루션 # 1을 개선하여 각 지점에서 더 이상 오른쪽에있는 나머지 지점을 반복 할 필요가 없습니다.복잡성이 다음과 같이 향상됩니다. O (w * h)!

메모리 사용량은 동일하게 유지됩니다 : O (w * h).

이것에서 무엇을 얻을 수 있습니까?

알고리즘과 코딩 기술 외에

알고리즘에는 많은 변형이있을 수 있으며, 가장 먼저 생각 해낸 알고리즘은 일반적으로 가장 효율적이지 않습니다.복잡성 분석 및 프로그래밍 기술에 대한 이해는 큰 차이를 만들 수 있습니다.이 실현의 중요성은 프로그래밍뿐만 아니라 삶의 거의 모든 것을 수행하는 데까지 확장됩니다. 삶의 모든 것이 알고리즘이기 때문입니다.