As I accumulate more experience in coding and life in general, one of the things among my observations that stood out to me is that, whenever there is a problem to be solved, there usually exists a very intuitive solution to it. Sometimes this solution happens to be efficient, sometimes grossly suboptimal. This is especially noticeable in algorithms, because an algorithm is often times a conceptualization of a real life problem, and through the algorithm the essential elements of the problem is kept, allowing us to tackle the problem directly.

The largest rectangle in a matrix is one such problem, in my opinion. Here is a brief description of the problem.

Problem

I have a board of red and blue dots, would like to find a biggest rectangle formed by the blue dots:

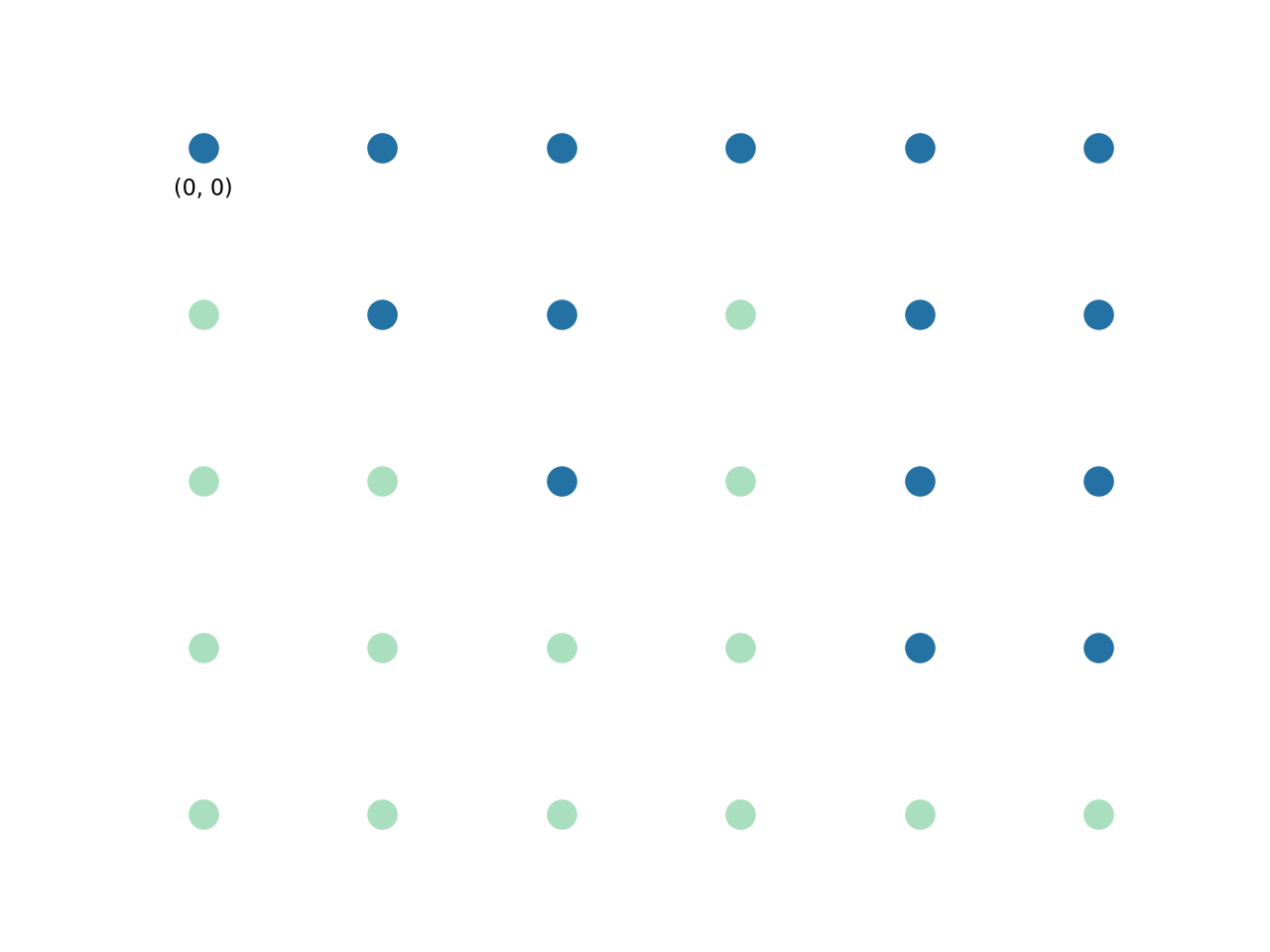
In this example, it’s easy to tell that the largest rectangle formed by the blue dots has a size of 8.

But let’s figure out a way to do this algorithmically.

Solution #1

How to do this simply

The first time I tried out this problem, I thought to myself:

Well, it looks like I probably need to iterate through every point in the matrix, and at each point, I need to find the largest rectangle containing that point. I’ll compare that rectangle to the size of the rectangles I have already found. If the new one is bigger, I’ll keep it, otherwise I move on to the next point.

This sounds great, but there is a problem with it. How do I find the largest rectangle containing a particular point. Nothing comes to mind that would help me solve this problem.

What if I just want to find the largest rectangle that has the current point as its top left corner? I think this is a more manageable problem.

In order for me to figure that out, I’ll loop through each point to the right of my current point, at each point I find the maximum height of blue dots, if it’s smaller than the height at the current point, I’ll update the current point height to the new height and find the size of the new rectangle, if it’s a bigger rectangle I’ll update the max size.

Let’s apply this procedure to our example.

Suppose I have looped to point (1, 0):

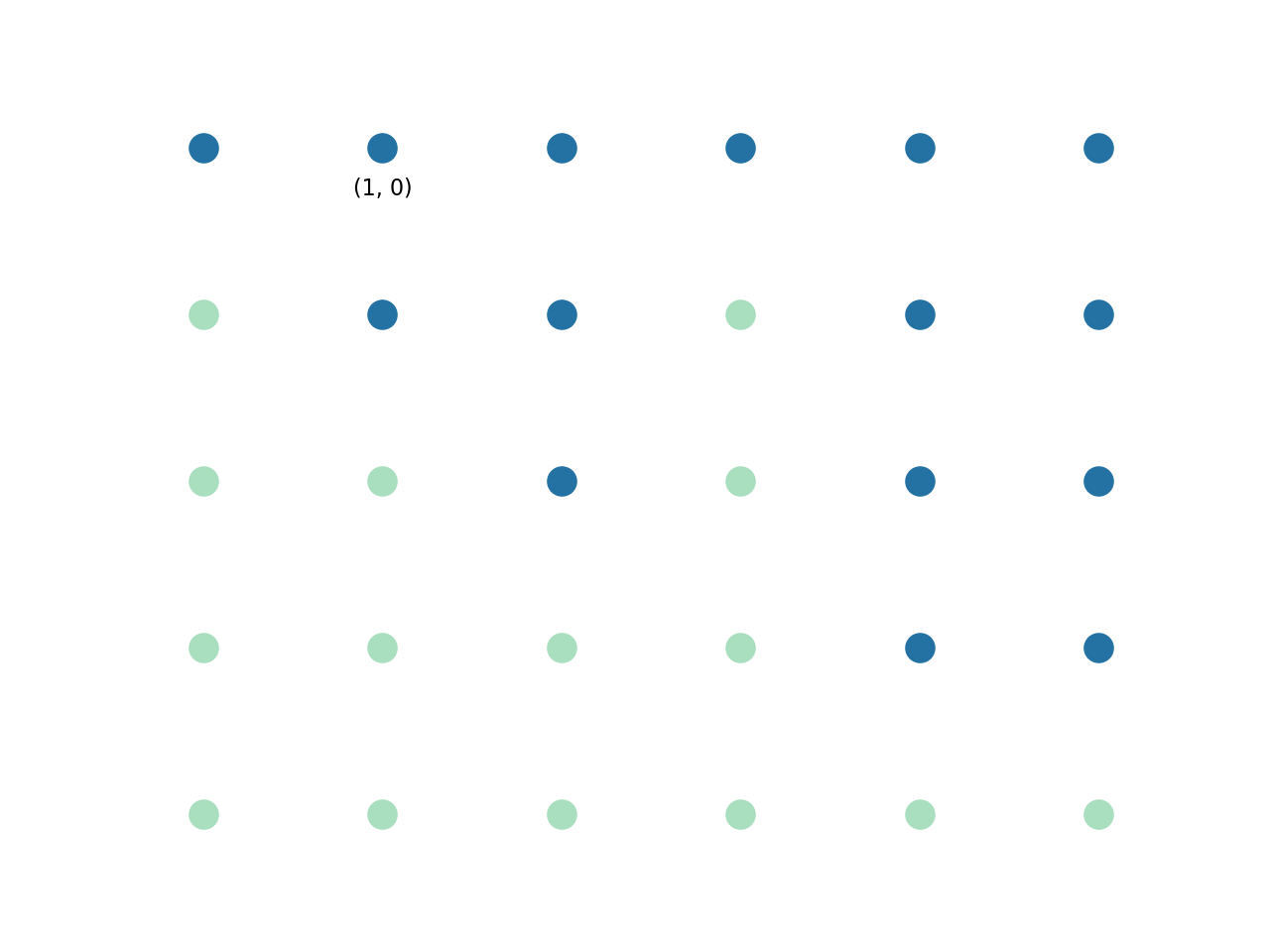
I find the height of my current point, which is 2, the largest rectangle with (1, 0) as top right corner given this information is also 2.

(1, 0): height = 2, max_rectangle = 2.

I iterate through every point to the right:

Point (2, 0) has a height of 3, but it’s larger than the starting point, so the height is still 2. But now we know that we can have a rectangle of size 2 * 2 = 4:

(2, 0): height = 2, max_rectangle = 4

Point (3, 0) has a height of 1, it’s smaller than current height, so we update current height to 1, the rectangle that can be created is: 1 * 3 = 3, but the current max is 4, so we ignore it:

(3, 0): height = 1, max_rectangle = 4

Going through the same process for the rest of points:

(4, 0): height = 1, max_rectangle = 4

(5, 0): height = 1, max_rectangle = 5

we find the largest rectangle with top right corner of (1, 0) to be of size 5.

Let’s put this into code:

def find_max001(matrix):

    width = len(matrix[0])
    height = len(matrix)

    # max width and max height at the a point
    # uses memorization and dynamic programming
    max_matrix = [[None for v in row] for row in matrix]
    def get_max(i, j):
        if i >= width:
            return 0, 0
        elif j >= height:
            return 0, 0
        elif max_matrix[j][i] is not None:
            return max_matrix[j][i]
        elif matrix[j][i] == 0:
            max_matrix[j][i] = (0, 0)
            return max_matrix[j][i]

        max_down = get_max(i, j + 1)
        max_right = get_max(i + 1, j)

        max_matrix[j][i] = (max_right[0] + 1,
                            max_down[1] + 1)
        return max_matrix[j][i]

    max_rect = 0
    for i in range(width):
        for j in range(height):
            rect = get_max(i, j)
            cur_max = rect[1]
            for k in range(1, rect[0]):
                cur_max = min(cur_max, get_max(i+k, j)[1])

            max_rect = max(max_rect, cur_max * rect[0])

    return max_rect
def problem003(solver):

    m001 = [
        [1, 1, 1, 1, 1, 1],
        [0, 1, 1, 0, 1, 1],
        [0, 0, 1, 0, 1, 1],
        [0, 0, 0, 0, 1, 1],
        [0, 0, 0, 0, 0, 0]
    ]

    res1 = solver(m001)
    print(f'res1: {res1}')
def test003():
    solver = find_max001
    problem003(solver)
test003()
# res1: 8

Performance of Solution #1

What is the complexity of the algorithm?

Since we are looping through each point, the complexity is at least w * h. Luckily we are able to use memoization and dynamic programming technique to find the height at each point, so they don’t add to the complexity.

At each point we are looping through the width of the matrix to find the largest rectangle at that point, this slows the complexity to w*h*w.

So the complexity is: O(w²*h)

Since we are also using a map to store width and height at each point:

memory usage is: O(w*h).

Solution #2

How to improve the algorithm?

Is there a way to reduce the w² term in complexity?

It turns out, there is.

Let’s go back to our example:

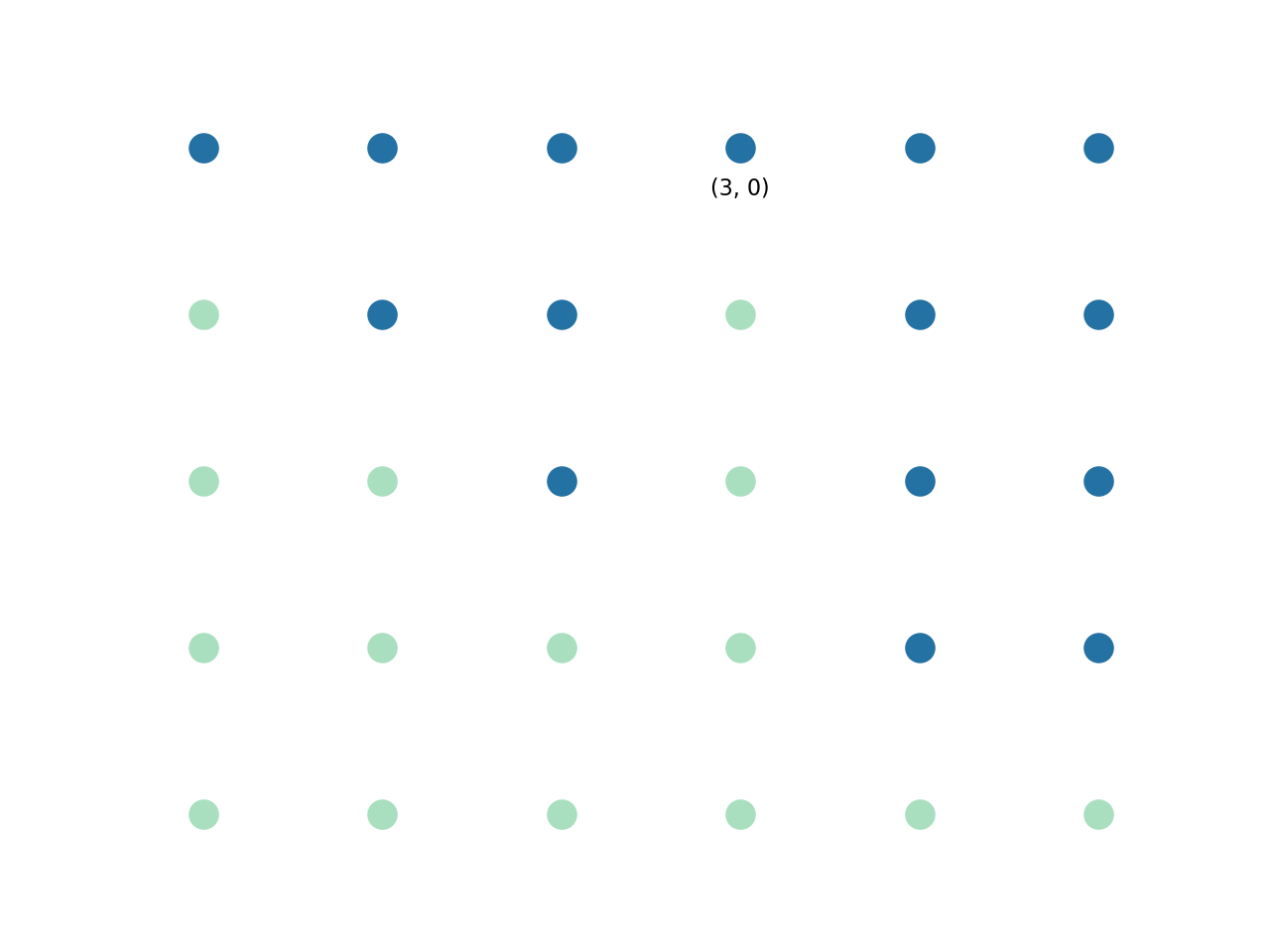
Suppose now we are looping through the first row.

From (0, 0), (1, 0), (2, 0) the height keeps increasing 1, 2, 3. We keep a list:

[(0, 0: 1), (1, 0: 2), (2, 0: 3)]

At position (3, 0), height drops to 1. What does this new information tell us?

Quite a bit, actually. Given this information, we can say for certain that a rectangle with top left corner at position (2, 0) with height 3 can only have a maximum size of 3.

We can also say for certain that a rectangle with top left corner at position (1, 0) with height 2 can only have a maximum size of 4.

After process the two points, we can remove them permanently, but we need to add a new point, at (1, 0) (note, not at (3, 0)), with height 1:

[(0, 0: 1), (1, 0: 1)]

Essentially what we are doing is trimming the height of (2, 0) and (1, 0) to equal to the height of (3, 0).

Moving on this way till the end of the row, we do not encounter any more drop in height.

[(0, 0: 1), (1, 0: 1), (5, 0: 4), (4, 0: 4)]

We can then process the rest of the rows:

(5, 0) max_rectangle = 4

(4, 0) max_rectangle = 4 * 2 = 8

(1, 0) max_rectangle = 1 * 5= 5

(0, 0) max_rectangle = 1 * 6 = 6

So the max_rectangle after processing the first row is 8, and we have only looped 6 points! This means the complexity of the algorithm is now w*h!

Below is the algorithm in code:

from collections import deque

def find_max002(matrix):

    width = len(matrix[0])
    height = len(matrix)

    # max depths
    max_matrix = [[None for v in row] for row in matrix]

    def get_max(i, j):
        if i >= width:
            return 0, 0
        elif j >= height:
            return 0, 0
        elif max_matrix[j][i] is not None:
            return max_matrix[j][i]
        elif matrix[j][i] == 0:
            max_matrix[j][i] = (0, 0)
            return max_matrix[j][i]

        max_down = get_max(i, j + 1)
        max_right = get_max(i + 1, j)

        max_matrix[j][i] = (max_right[0] + 1, max_down[1] + 1)
        return max_matrix[j][i]

    def get_rect(stack, j):
        cur_idx = stack.pop()
        cur_max = cur_idx[1] * (j - cur_idx[0])
        print(f"cur_max at {cur_idx[0]}: {cur_max}")
        return cur_max

    max_rect = 0
    for i in range(width):

        # implement the algorithm with stack
        stack = deque()
        stack.append((-1, 0))
        for j in range(height):
            rect = get_max(i, j)
            cur_width = rect[0]
            cur_idx = j
            while stack[-1][1] > cur_width:
                cur_idx = stack[-1][0]
                max_rect = max(max_rect,
                               get_rect(stack, j))
            stack.append((cur_idx, cur_width))

        while len(stack) > 1:
            max_rect = max(max_rect, get_rect(stack, height))

    return max_rectdef test004():

    solver = find_max002

    problem003(solver)
test004()
# res1: 8

Notice in order to implement the removal of points (2, 0) and (1, 0) after we reach (3, 0), we use a stack data structure to push and pop points efficiently.

Complexity of Solution #2

As mentioned earlier, we have improved upon solution #1 so that at each point, we don’t have to loop through the rest of the points to its right anymore. The complexity improves to: O(w*h)!

The memory usage remains the same: O(w*h).

What to get out of this?

besides the algorithm and coding techniques

An algorithm can have many variations, the first one you come up with is usually not the most efficient. An understanding of complexity analysis and programming techniques can make a big difference. The importance of this realization extends not only to programming, but to doing almost everything in life, because everything in life is an algorithm.