This one doesn’t need much introduction. Thousands of articles, papers have been written and a few wars have been fought on Bayesian vs Frequentism. In my experience, most folks start with usual linear regression and work their way up to build more complex models and only a few get to dip their feet in the holy pool of Bayes and this lack of opportunity along with the terseness of the topic punches holes in the understanding, at least for me it did.

I don’t want to be bogged down by too many mathematical equations and want to have an intuitive understanding of what, why, and where of the Bayesian statistics. This is my humble attempt to do so.

Building intuition for Bayesian processes

Let’s build an intuition for Bayesian analysis. I believe one time or the other you might have been sucked in the debate between Frequentism vs Bayesian. There is a lot of literature out there that can explain the difference between the two approaches of statistical inference.

In short, Frequentism is the usual approach of learning from the data, using p-values to measure the significance of variables. The frequentist approach is about point estimates. If my linear equation is:

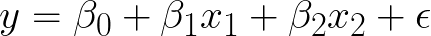
y is the response variable, x₁, x₂ are the dependent variables. β₁ and β₂ are the coefficients that need to be estimated. β₀ is the intercept term; If x₁ changes by 1 unit then y is affected by β₁ units e.g. if x₁ is 1 and β₁ is 2 then y will be affected by 2 units. Usual linear stuff. The thing to note here is that the regression equation estimates values of various β, that best explain the data at hand, based on minimising the sum of squared errors(line of best fit) and the estimated values are singular point i.e. there will be one value for β₀, one for β₁, and one for β₂, and so on. The estimated values of β are known as the maximum likelihood estimate of β because it is the value that is the most probable given the inputs, x, and output, y.

Bayesian differs from the frequentist approach in the fact that apart from the data, it takes the prior knowledge of the data into account. That’s where the beef lies between the two groups. Frequentists take data as the gospel while Bayesians think there is always something that we know about the system and why not use it in the estimation of the parameters.

The data along with the prior knowledge are taken together to estimate what’s known as the posterior and it is not a single value but a distribution. Bayesian methods estimate a posterior distribution of the model parameters, not a single best value as is the case in the frequentist approach.

The priors that we choose for the model parameters are not single values but they are distributions as well, they could be Normal, Cauchy, Binomial, Beta or any other distribution deemed fit according to our guess.

I hope you are aware of the vernacular and script of Bayes’ theorem

(Feel free to skip this section if you already understand Bayes’s Theorem)

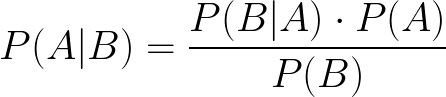
Although, it is quite self-explanatory but let me just explain with the help of a very basic example.

P(A|B) refers to the probability of A given B has already happened. e.g. A random card is drawn from a deck of 52 cards, what is the probability that it is King GIVEN we drew a hearts card?

A = Card is King, B = Card is from Hearts suite.

P(A= King|B = Hearts)

P(A) = P(King) = 4/52 = 1/13

P(B) = P(Hearts) = 13/52 = 1/4

P(B|A) = P(Hearts| King) = Probability of getting a Hearts card GIVEN it is King = 1/4 (There are 4 kings in a set of 52 and you can select only one king of hearts out of those 4 kings)

Putting it all together, P(A|B) = (1/4). (1/13) / (1/4) = 1/13, so there are 1 in 13 chances to get a king given it is hearts.

I chose this simple example because it doesn’t really need Bayes’ rule to solve so even the beginners can think about it intuitively; Given it is a hearts’ card, the probability of getting a king is 1 out of 13.

How does the Bayesian approach include prior information?

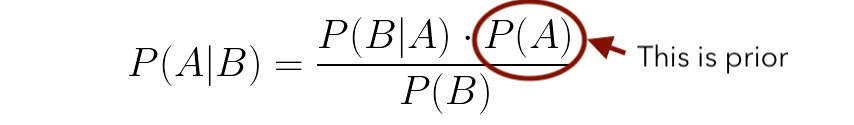
P(A) is the value that we have approximated or what we have data on. In the above example, P(A) is the probability of getting a king irrespective of the suite. We know that the probability of getting a king is 1/4, so instead of starting with a clean slate, we are providing a value of 0.25 to the system.

By the way, Thomas Bayes didn’t come up with the above equation Laplace did. Bayes wrote a paper “An Essay towards solving a Problem in the Doctrine of Chances” on his thought experiments. After Bayes’ death, his friend Richard Price found the paper and after a few editions by him, the paper was read at the Royal Society of London.

For the Bayesian inference:

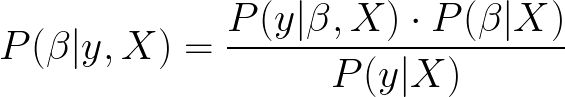
P(β|y, X) is the called the posterior distribution of the model parameters, β, given the data X and y, where X is input and y is output.

P(y|β, X) is the likelihood of the data which is multiplied by the prior probability of the parameters, P(β|X), and divided by P(y|X) which is known as a normalization constant. This normalisation parameter is required to make the sum of values in P(β|y, X) equals 1.

In nutshell, we are using our prior information about the model parameters and the data to estimate posterior.

Give yourself a pat on the back if you have made it this far! 🙂

A lot of Bayesian aligned thinkers attribute the solution of Enigma to Alan Turing. Well, yes, he did indeed build the probabilistic model but Polish Mathematicians helped him. Long before the war, Polish mathematicians had solved the enigma using Mathematical approach when Britishers were still trying to solve it linguistically. Hail Marian Rejewski!

Moment of truth through an example

Let’s see if we can understand what we learned above with some simple example to build our intuition.

Let’s toss a coin 20 times, 1 is heads and 0 is tails. Here are the outcomes of the coin throws:

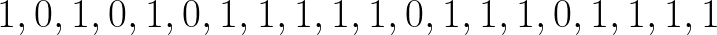
The mean of this data is 0.75; in other words, there are 75% chances of getting heads i.e. 1 rather than getting a tail i.e. 0

By the way, any process that has canonically only two outcomes 0 or 1is referred to as Bernoulli process.

Taking a frequentist approach, it seems the coin is biased i.e. if we toss it one more time then according to frequentist estimates, it is more likely (75% of the times)that the coin will turn up heads i.e.1.

Although, most coins aren’t biased and the probability of getting a 1 or a 0 should be 50%. According to the central limit theorem, if we had tossed the coin infinite times then the probabilities would have lined up to be 0.5 for both head and tails. Real-life is quite different from theorems, no one is going to toss a coin infinite times; we have to make decisions on whatever data is available to us.

That’s where the Bayesian approach is helpful. It gives us the freedom to include the priors(our initial beliefs) and that’s what we will do to the coin flip data. If we don’t have any information about the priors then we can use a completely uninformative uniform distribution — in practice, the results of the uniform distribution will be same as the frequentist approach because we are telling our model that each possibility is equally likely.

Non-Bayesian(Frequentist) = Bayesian with a uniform prior

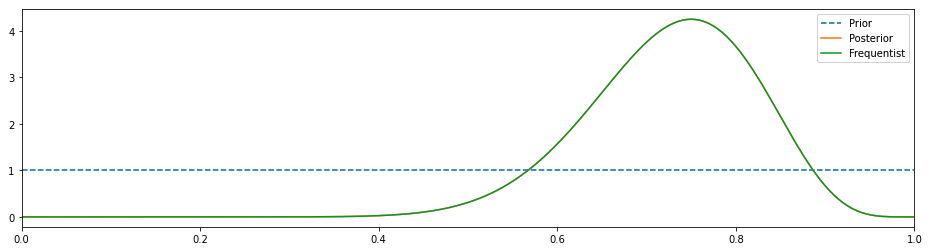
In the chart above, posterior and frequentist results coincide and it peaks at around 0.75( just like the frequentist approach). Prior is a straight line because we assumed that a uniform distribution. In this case, the green distribution is actually a likelihood.

I believe we can do better than that. Let’s change our prior to something more informed, maybe a beta distribution and observe the results.

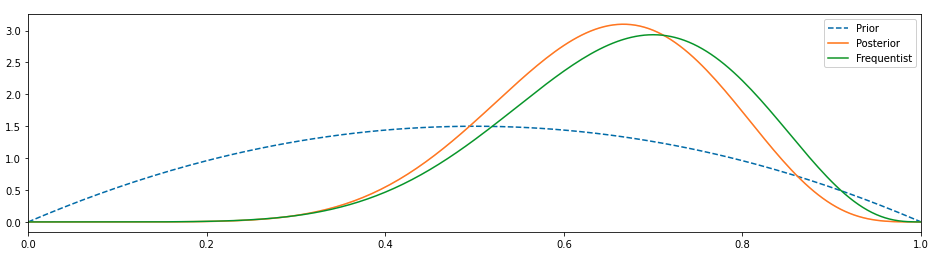
This seems better. Our prior has changed and because of that the posterior has moved towards the left, it isn’t near the 0.5 value but it isn’t at least coincidental with the frequentist at 0.75.

We can improve it further by tweaking a few params of our prior distribution so that it becomes more opinionated.

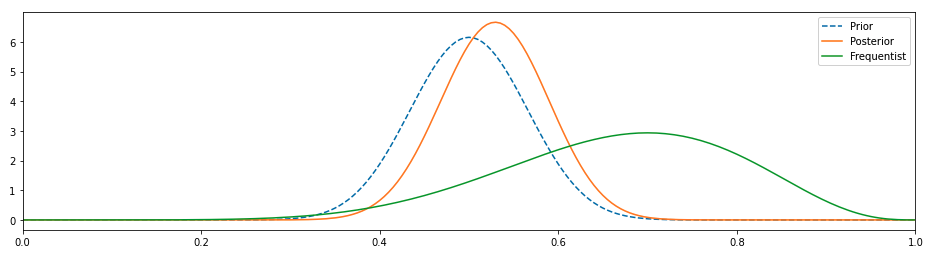
This seems much better, the posterior has shifted as we have changed our prior and is much more in line with the fact that an unbiased coin will yield heads 50% of the time and tales rest of the time.

Our existing knowledge about the coin had a major impact on the results and that makes sense. It is the polar opposite to the frequentist approach in which we assume that we know NOTHING about the coin and these 20 observations are the gospel.

Conclusion

So you see how through Bayesian, despite having a paucity of data, we were able to reach the approximately right conclusion when we included our initial beliefs in the model. Bayes’ rule is behind the intuition of Bayesian statistics(such an obvious statement to make) and it provides an alternative to frequentism.

1. The Bayesian approach incorporates prior information and that can be a solid tool when we have limited data.

2. The approach seems intuitive — estimate what your solution would be and improve that estimate as you gather more data.

Please understand that it doesn’t mean that Bayesian is the best approach for solving all data science problems; It is only one of the approaches and it would be fruitful to learn both Bayesian and Frequentist methods rather than fighting the crusades between these schools of thoughts.

With great power comes great responsibility. Take everything with a grain of salt. Although there are apparent advantages of Bayesian methods, it is much easier to produce highly biased results. One can choose a prior that can shift the entire results. As an example, it is much easier and cheaper to choose the ‘right’ prior than invest millions of dollars in research and development of safer and effective drugs in the pharmaceutical world. When billions of dollars are on the line, it’s easier to publish mediocre studies in predatory journals and use them as your prior.

Further reading:

Johnson, S. (2002). Emergence: The connected lives of ants, brains, cities, and software. Simon and Schuster.

Happy reading & stay curious!