베이지안 통계에 대한 제로 수학 소개
통계 세계의 십자군 해독 — 베이지안 대 빈도주의
이것은 많은 소개가 필요하지 않습니다.수천 개의 기사, 논문이 작성되었으며 베이지안 대 빈도주의에 대한 몇 가지 전쟁이 벌어졌습니다.내 경험상 대부분의 사람들은 일반적인 선형 회귀로 시작하여 더 복잡한 모델을 구축하기 위해 노력하고 소수만이 신성한 Bayes 풀에 발을 담그고 주제의 간결함과 함께 이러한 기회가 부족하여 구멍을 뚫습니다.이해에서 적어도 나에게는 그랬다.
나는되고 싶지 않다 너무 많은 수학적 방정식으로 인해 어려움을 겪고 베이지안 통계의 내용, 이유 및 위치를 직관적으로 이해하고자합니다.이것은 저의 겸손한 시도입니다.
베이지안 프로세스에 대한 직관 구축
베이지안 분석에 대한 직관을 구축해 보겠습니다.나는 한 번 또는 다른 당신이 Frequentism과 Bayesian 사이의 논쟁에 빠졌을 것이라고 믿습니다.통계적 추론의 두 가지 접근 방식의 차이점을 설명 할 수있는 많은 문헌이 있습니다.
요컨대빈도주의변수의 유의성을 측정하기 위해 p- 값을 사용하여 데이터에서 학습하는 일반적인 접근 방식입니다.빈도주의 접근법은 포인트 추정에 관한 것입니다.내 선형 방정식이 다음과 같으면
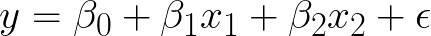
y는 반응 변수, x₁, x₂는 종속 변수입니다.β₁ 및 β₂는 추정해야하는 계수입니다.β₀은 절편 항입니다.x₁이 1 단위 씩 변하면 y는 β₁ 단위의 영향을받습니다.x₁이 1이고 β₁이 2이면 y는 2 단위의 영향을받습니다.일반적인 선형 물건.여기서 주목해야 할 점은 회귀 방정식이 다양한 β의 값을 추정한다는 것입니다.이 값은 제곱 오차 (최적 적합 선)의 합을 최소화하여 현재 데이터를 가장 잘 설명하며 추정 된 값은 단일 점입니다.β₀에 대한 값, β₁에 대한 값, β₂에 대한 값 등.β의 추정값은최대 가능성 추정입력 값 x와 출력값 y를 고려할 때 가장 가능성이 높은 값이기 때문입니다.
베이지안 데이터와는 별도로 데이터에 대한 사전 지식을 고려한다는 점에서 빈도주의 접근 방식과 다릅니다.여기에서 두 그룹 사이에 쇠고기가 놓여 있습니다.빈도 주의자들은 데이터를 복음으로 받아들이는 반면 베이지안 사람들은 우리가 시스템에 대해 항상 알고있는 것이 있고 매개 변수 추정에 그것을 사용하지 않는 이유가 있다고 생각합니다.
사전 지식과 함께 데이터는 사후라고 알려진 것을 추정하기 위해 함께 취해지며 단일 값이 아니라 분포입니다.베이지안 방법은 빈도주의 접근법의 경우와 같이 단일 최상의 값이 아닌 모델 매개 변수의 사후 분포를 추정합니다.
모델 매개 변수에 대해 선택한 사전은 단일 값이 아니지만 분포이기도합니다. 정규, 코시, 이항, 베타 또는 추측에 따라 적합하다고 간주되는 다른 분포 일 수 있습니다.
베이 즈 정리의 토착어와 대본을 알고 계시길 바랍니다.
(베이 즈 정리를 이미 이해하고 있다면이 섹션을 건너 뛰어도됩니다.)
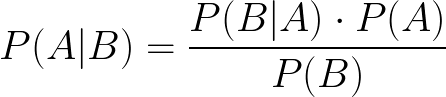
비록 그것은 매우 자명하지만 아주 기본적인 예의 도움으로 설명하겠습니다.
P (A | B)는 B가 이미 발생한 경우 A의 확률을 나타냅니다.예 :52 장의 카드 더미에서 무작위 카드를 가져옵니다.킹 GIVEN이 하트 카드를 뽑았을 확률은 얼마입니까??
A = 카드는 왕, B = 카드는 하트 스위트에서 가져온 것입니다.
P (A = 왕 | B = 하트)
P (A) = P (왕) = 4/52 = 1/13
P (B) = P (하트) = 13/52 = 1/4
P (B | A) = P (하트 | 킹) = 하트 카드를받을 확률 주어진 킹 = 1/4 (52 개 세트에는 4 개의 킹이 있으며 그중 하나의4 왕)
종합하면 P (A | B) = (1/4).(1/13) / (1/4) =1/13, 그래서 13 분의 1의 기회는 그것이 하트라면 왕을 얻을 수 있습니다.
저는이 간단한 예를 선택했습니다. 왜냐하면 베이 즈의 규칙을 풀 때 실제로 필요하지 않기 때문에 초보자도 직관적으로 생각할 수 있습니다.하트 카드라면 왕이 될 확률은 13 점 만점에 1 점입니다.
베이지안 접근 방식에는 사전 정보가 어떻게 포함됩니까?
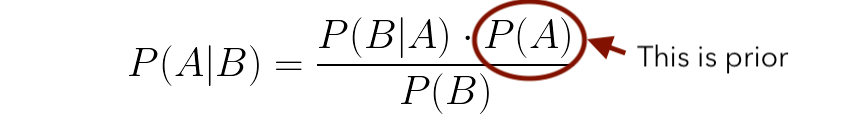
P (A)는 근사치 또는 데이터가있는 값입니다.위의 예에서 P (A)는 스위트에 관계없이 킹을 얻을 확률입니다.우리는 왕을 얻을 확률이 1/4이라는 것을 알고 있으므로 깨끗한 슬레이트로 시작하는 대신 시스템에 0.25의 값을 제공합니다.
그건 그렇고, Thomas Bayes는 Laplace가 한 위의 방정식을 생각해 내지 못했습니다.Bayes는“기회 교리의 문제 해결에 대한 에세이”그의 생각 실험에.Bayes가 사망 한 후 그의 친구 Richard Price가이 논문을 발견하고 몇 번의 판본을 읽은 후 런던 왕립 학회에서이 논문을 읽었습니다.
베이지안 추론의 경우 :
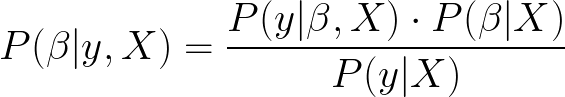
P (β | y, X)는 데이터 X와 y가 주어지면 모델 매개 변수 β의 사후 분포라고합니다. 여기서 X는 입력이고 y는 출력입니다.
P (y | β, X)는 데이터가 다음과 같이 곱해질 가능성입니다.사전 확률매개 변수의 P (β | X)를 정규화 상수라고하는 P (y | X)로 나눕니다.이 정규화 매개 변수는 P (β | y, X) 값의 합이 1이되도록하는 데 필요합니다.
간단히 말해서, 모델 매개 변수에 대한 이전 정보와 사후를 추정하기 위해 데이터를 사용하고 있습니다.
여기까지왔다면 등을 가볍게 두 드리십시오!:)
베이지안의 많은 사상가들은 Enigma의 해결책을 Alan Turing에 기인합니다.네, 그는 실제로 확률 모델을 만들었지 만 폴란드 수학자들이 그를 도왔습니다.전쟁이 있기 오래 전 폴란드의 수학자들은 영국인들이 여전히 언어 학적으로 그것을 풀려고 할 때 수학적 접근법을 사용하여 수수께끼를 풀었습니다.빗발마리안 레유 스키!
Moment of truth through an example
우리의 직관을 구축하기위한 몇 가지 간단한 예를 통해 위에서 배운 것을 이해할 수 있는지 봅시다.
동전을 20 번 던집니다. 1은 앞면, 0은 뒷면입니다.동전 던지기의 결과는 다음과 같습니다.
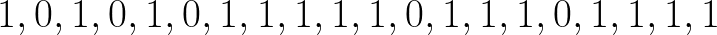
이 데이터의 평균은 0.75입니다.즉, 꼬리 (0)를 얻는 것보다 앞면 (1)을 얻을 확률이 75 %입니다.
그건 그렇고, 정규적으로 두 개의 결과 0 또는 1 만있는 모든 프로세스를베르누이 프로세스.
빈도 주의적 접근 방식을 취하면 동전이 편향된 것 같습니다.
하지만 대부분의 코인은 편향되지 않으며 1 또는 0을 얻을 확률은 50 % 여야합니다.중앙 극한 정리에 따르면 동전을 무한히 던졌다면 확률은 앞면과 뒷면 모두 0.5가 될 것입니다.실생활은 정리와는 상당히 다르며, 아무도 동전을 무한대로 던지지 않을 것입니다.우리가 사용할 수있는 데이터에 대해 결정을 내려야합니다.
바로 베이지안 접근 방식이 도움이됩니다.그것은 우리에게 사전 (우리의 초기 신념)을 포함 할 수있는 자유를 제공하며 이것이 우리가 동전 던지기 데이터에 할 일입니다.사전에 대한 정보가없는 경우 완전히 정보가없는 균일 분포를 사용할 수 있습니다. 실제로 균일 분포의 결과는 각 가능성이 동일 할 가능성이 있음을 모델에 알리기 때문에 빈도주의 접근 방식과 동일합니다.
Non-Bayesian (Frequentist) = 균일 사전이있는 베이지안
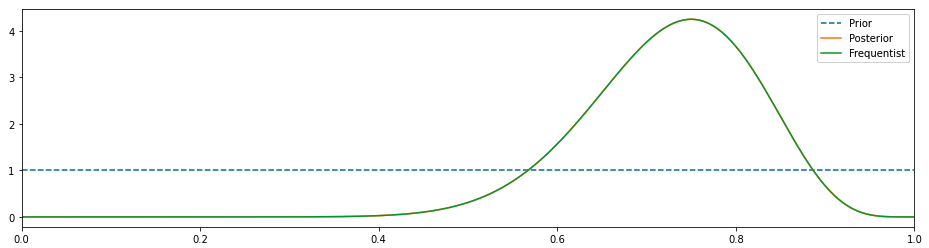
위의 차트에서 사후 및 빈도주의 결과는 일치하며 약 0.75에서 정점에 이릅니다 (빈도주의 접근 방식과 동일).Prior는 균등 분포를 가정했기 때문에 직선입니다.이 경우 녹색 분포는 실제로 가능성입니다.
나는 우리가 그것보다 더 잘할 수 있다고 믿습니다.더 많은 정보, 아마도 베타 배포판으로 이전을 변경하고 결과를 관찰합시다.
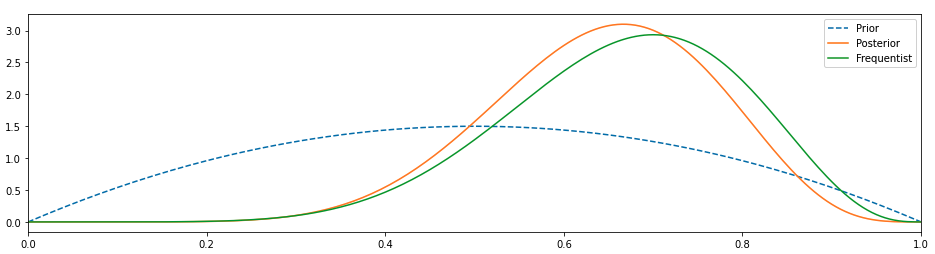
이것은 더 좋아 보인다.우리의 사전이 변경되었고 사후가 왼쪽으로 이동했기 때문에 0.5 값에 가깝지는 않지만 적어도 0.75에서 빈도 주의자와 일치하지는 않습니다.
우리는 이전 배포판의 몇 가지 매개 변수를 조정하여 더 많은 의견을 제시함으로써 더 개선 할 수 있습니다.
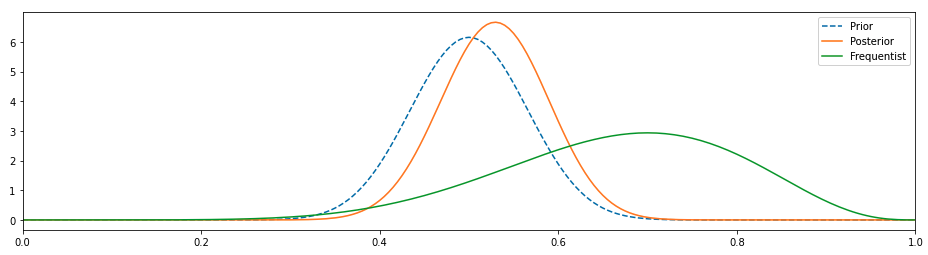
이것은 훨씬 더 좋아 보이며, 우리가 이전을 변경함에 따라 사후가 바뀌었고, 편향되지 않은 동전이 시간의 50 %를 차지하고 나머지 시간 동안 이야기를 할 것이라는 사실과 훨씬 더 일치합니다.
코인에 대한 우리의 기존 지식은 결과에 큰 영향을 미쳤으며 이는 의미가 있습니다.그것은 우리가 동전에 대해 아는 것이없고이 20 가지 관찰이 복음이라고 가정하는 빈도 주의적 접근과 정반대입니다.
Conclusion
따라서 데이터가 부족함에도 불구하고 베이지안을 통해 모델에 초기 신념을 포함했을 때 거의 올바른 결론에 도달 할 수 있었던 방법을 알 수 있습니다.Bayes의 규칙은 Bayesian 통계의 직관 뒤에 있으며 (이러한 명백한 진술) 빈도주의에 대한 대안을 제공합니다.
- 베이지안 접근 방식은 사전 정보를 통합하며 데이터가 제한적일 때 견고한 도구가 될 수 있습니다.
2. 접근 방식은 직관적 인 것 같습니다. 솔루션이 무엇인지 추정하고 더 많은 데이터를 수집할수록 해당 추정치를 개선합니다.
베이지안이 모든 데이터 과학 문제를 해결하기위한 최선의 접근 방식이라는 의미는 아닙니다.이는 접근 방식 중 하나 일 뿐이며 이러한 사고 학파 간의 십자군 전쟁에 맞서기보다는 베이지안과 빈도주의 방법을 모두 배우는 것이 유익 할 것입니다.
W큰 힘에는 큰 책임이 따른다.모든 것을 소금 한 알로 가져 가십시오.베이지안 방법의 명백한 이점이 있지만 고도로 편향된 결과를 생성하는 것이 훨씬 쉽습니다.전체 결과를 바꿀 수있는 사전을 선택할 수 있습니다.예를 들어, 제약 업계에서 안전하고 효과적인 약물을 연구하고 개발하는 데 수백만 달러를 투자하는 것보다 먼저 ‘올바른’것을 선택하는 것이 훨씬 쉽고 저렴합니다.수십억 달러에 달하는 경우 약탈적인 저널에 평범한 연구를 게시하고이를 이전 연구로 사용하는 것이 더 쉽습니다.
추가 읽기 :
Johnson, S. (2002).출현 : 개미, 뇌, 도시 및 소프트웨어의 연결된 삶.사이먼과 슈스터.
즐거운 독서 & amp;호기심을 가지세요!
