Cryptocurrency 시장에서 주문 장 불균형의 가격 영향
190 만 건의 주문서 관찰에서 무엇을 배울 수 있습니까?
불균형 주문서가 책의 얇은면으로 가격 변동을 유발하는지 조사합니다.즉,이 가설에 의해 지정가 주문 장부가 입찰 측에 비해 호가 측에 게시 된 양이 많을 때 가격이 하락하고, 주문 장부가 입찰 측에서 더 무거 우면 가격이 상승합니다.우리는이 가설을 테스트하고 주문 장 불균형 정보를 이용하여 ETHUSD 시장의 가격 변동을 수익성있게 예측할 수 있는지 평가합니다.
주문 장 불균형
우리는 문헌을 따릅니다.Cartea et al.(2015), 주문 장 불균형을 다음과 같이 정의하십시오.
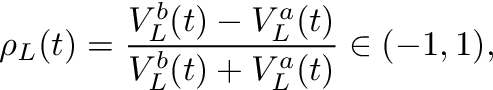
어디티시간을 인덱싱하고,V입찰 (위 첨자비) 또는 질문 (위첨자ㅏ) 및엘ρ를 계산하기 위해 고려되는 주문서의 깊이 수준입니다..그림 1은 불균형을 계산하는 방법의 예를 보여줍니다.ρ주어진 주문서에 대해.
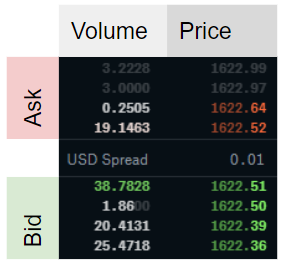
ㅏρ-1에 가까운-값은 시장 조성자가 입찰 수량에 비해 대량의 수량을 게시 할 때 획득됩니다.ρ 값이 1에 가까우면 요청 측에 비해 주문서의 입찰 측에 대량이 있음을 의미합니다.불균형이 0이면 주문서가 주어진 수준에서 완벽하게 균형을 이룹니다.엘.가설은 낮은 불균형 숫자 (& lt; 0)는 음의 수익을 의미하고, 높은 불균형 숫자 (& gt; 0)는 양의 수익을 의미합니다. 즉, 가격이 불균형 방향으로 이동 함ρ.
연구자들은 주식 시장 데이터에서 무엇을 결론 내립니까?
Cont et al.(2014)미국 주식 데이터를 사용하여 주문 흐름 불균형의 가격 영향과 “주문 흐름 불균형”과 가격 변동 사이의 선형 관계가 있음을 보여줍니다.저자는 주문 흐름 불균형을 주어진 기간 동안 들어오는 주문을 집계하여 측정 된 공급과 수요 사이의 불균형으로 정의합니다.선형 모델의 R²는 약 70 %입니다.이 연구는 과거 주문 흐름 (불균형 측정을 초래 함)을 고려하고이를 동일한 기간 동안의 가격 변동과 비교합니다.따라서 결론은 주문 흐름 불균형이 미래 가격을 예측하는 것이 아니라 과거 기간 동안 계산 된 주문 흐름 불균형이 같은 기간 동안의 가격 변화를 설명한다는 것입니다.따라서이 연구는 미래 가격에 대한 현재 주문 흐름 불균형에 대한 직접적인 통찰력을 보여주지 않습니다.실란 티 예프 (2018)미디엄 기사에서 BTC-USD 주문서 데이터를 사용하여이 연구 결과를 확인합니다.
Lipton et al.(2013), 우리 불균형 측정ρ와L = 1다음 틱까지의 가격 변동은 주문 장 불균형의 선형 함수에 의해 잘 근사화 될 수 있지만
(1) 변경이 매도 매도 스프레드보다 훨씬 낮고
(2) 방법은 “그 자체로는 직접적인 통계적 차익 거래 기회를 제공하지 않습니다”.
Cartea et al.(2018)에 의해 측정 된 더 높은 주문 책 불균형을 발견하십시오ρ그 뒤에는 시장 주문량이 증가하고 불균형은 시장 주문이 도착한 직후 가격 변화를 예측하는 데 도움이됩니다.
그들의 책에서Cartea et al.(2015)과거 불균형과 가격 변동의 상관 관계가 괜찮은 특정 주식에 대해 존재합니다 (10 초 간격 동안 약 25 %).
스토이 코프 (2017)통합하는 중간 가격 조정을 정의합니다.
주문 장 불균형 및 매도 매도 스프레드.그는 결과가
가격 (중가 + 조정)은 중가 및 볼륨 가중 중가보다 중가의 단기 변동에 대한 더 나은 예측 변수입니다.이 연구에서 주문 장 불균형은 우리의 불균형과 약간 다릅니다. 특히 공식 (1)은 지명자에서 요청 볼륨을 제거하고 레벨을 고정하여 조정됩니다.엘이 방법은 현재 정보를 조건으로 미래의 중간 가격에 대한 기대치를 추정하며 수평선과 무관합니다.예측이 가장 정확한 경험적 지평은 평가 된 주식에 대해 3 ~ 10 초 범위입니다.조정 된 중간 가격은 제시된 데이터에 대한 입찰과 요청 사이에 존재하며, 이는 방법 자체가 통계적 차익 거래 방법을 제시하지 않지만 저자가 언급했듯이 알고리즘을 개선하는 데 사용할 수 있음을 나타냅니다.
이 연구에서는 최적의 매도 호가 가격 (L = 1),
우리는 더 긴 수평선을보고 순서를 계산하기 위해 깊이 5를 조사합니다.
불균형.이 연구의 데이터는 주식 시장 데이터를 사용합니다.
주목할만한 예외실란 티 예프 (2018), 우리는 암호 화폐 주문서를 조사합니다.
데이터
오더 북 데이터는 암호 화폐 거래소에서 공개 API를 통해 조회 할 수 있습니다.캔들 데이터 이외의 과거 데이터는 일반적으로 사용할 수 없습니다.따라서 2019 년 5 월부터 12 월까지 (2019–05–21 01:46:37 ~ 2019–12–18 18:40:59) 10 초 간격으로 Coinbase에서 ETHUSD에 대한 주문 장 데이터를 최대 5 단계까지 수집했습니다.이것은 1,920,617 개의 관측치에 해당합니다.데이터에 약간의 차이가 있습니다 (예 : 시스템 다운 타임으로 인해 분석에서 설명 함).두 개의 후속 주문서 관찰 간의 타임 스탬프 차이가 11 초보다 큰 592 개의 간격을 계산합니다.두 주문서 사이의 타임 스탬프는 연속적인 Websocket 스트림이 아닌 반복적 인 REST 요청을 사용하여 데이터를 수집했기 때문에 데이터에서 정확히 10 초가 아닙니다.
오더 북 불균형 분배
가격 변동과 주문 장 불균형 간의 관계를 살펴보기 전에 다양한 주문 장 수준에 대한 불균형 분포를 살펴 봅니다.
주문 장 불균형을 계산합니다.ρ모든 관측치와 방정식 1에 따라 5 가지 레벨에 대해 다음 속성을 찾습니다.
- 에서L = 1불균형은 종종 매우 뚜렷하거나 전혀 존재하지 않습니다.더 높이엘, 균형 잡힌 주문 장부가 더 빈번할수록 (즉,ρ≈0).
- 불균형은 자기 상관입니다.레벨이 깊을수록엘, 자기 상관이 높을수록
그림 2와 3에서 첫 번째 결과를, 그림 4에서 두 번째 결과를 제시합니다.
그림 2는 레벨 1에 대한 오더 북 불균형의 히스토그램을 보여줍니다.이 레벨에서 오더 북은 대부분 균형이 잡혀 있거나 (0에 가까움) 매우 불균형 (-1 또는 1에 가까움)되어 있습니다.
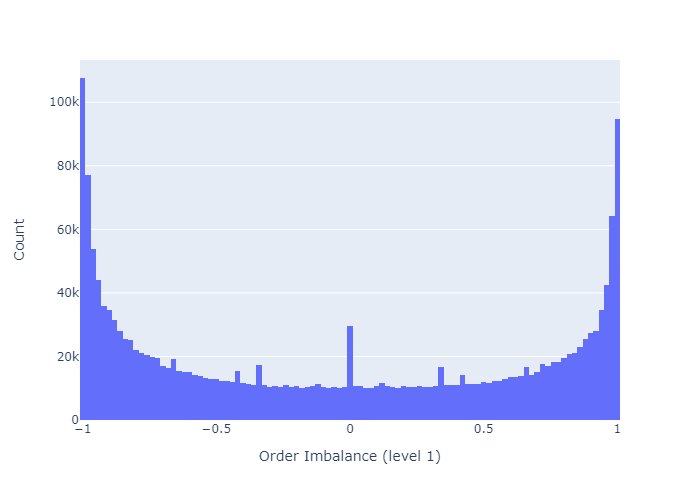
불균형을 계산하기 위해 주문 장 깊이를 늘리면 그림 3에서 볼 수 있듯이 주문 장의 균형이 더 높아집니다.
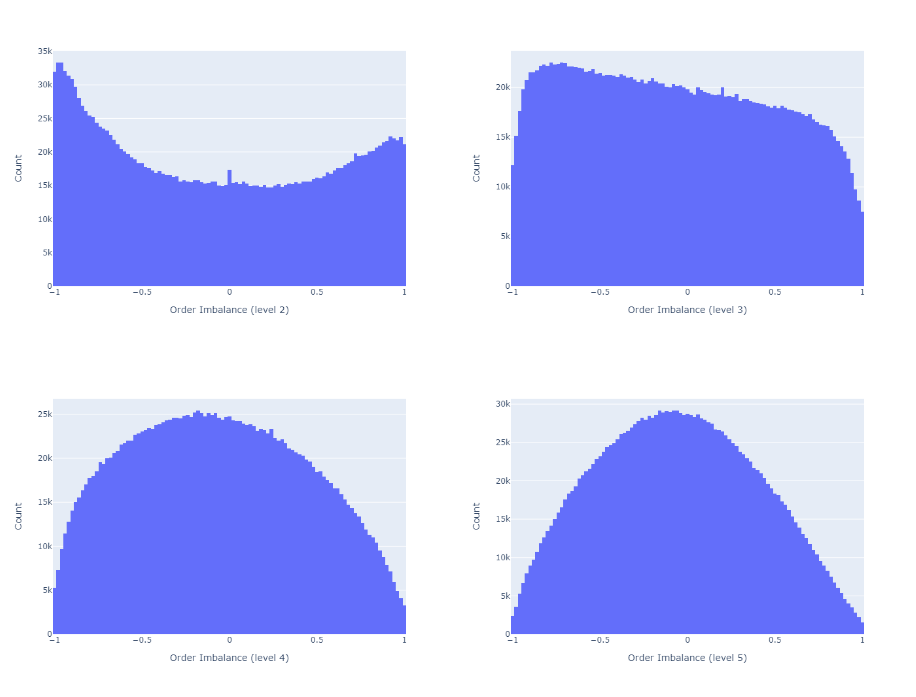
그림 4는 자기 상관 함수 (ACF)를 보여줍니다.일치Cuartea et al.(2015)불균형은 자기 상관성이 높다는 것을 알 수 있습니다.주어진 지연에 대한 상관 관계는 더 높은 경향이 있으며 주문 장 깊이가 더 큽니다.엘불균형 계산을 위해.
주문 장 불균형이 가격 변동을 예측하는 데 도움이됩니까?
이제 ρ와 미래 중간 가격의 상관 관계를 조사합니다.중간 가격은 최고 입찰 가격과 최저 요청 가격의 평균으로 정의됩니다.
먼저 주문 장 불균형을 관찰 할 때마다 중간 가격의 p- 기간 선행 로그 수익을 계산합니다.그런 다음 이러한 수익률과 기간 초에 관찰 된 주문 불균형 간의 상관 관계를 계산합니다.p-주기가 평균 11 초 (1주기 ≈ 10 초)보다 긴 관측치를 제거합니다.
그림 5와 6은 수익이 측정되는 기간의 함수로서 미래 수익률과 불균형의 상관 관계를 보여줍니다.우리는 다음과 같이 결론을 내립니다.
- 상관 관계가 낮습니다.
예 :Cont et al.(2014)가격 영향과 동일한 기간 동안의 주문 흐름 불균형 측정 사이에 약 70 %의 R²를보고합니다.선형 일 변량 회귀 모델의 경우R²는 상관 관계를 의미합니다.sqrt의(0.70) = 0.84.그러나 저자는 가격 인상을같은 기간주문 흐름 불균형으로 인해이 방법은 가격 예측을 제공하지 않습니다. - 불균형 측정ρ불균형 관찰에 가까운 가격에 대해 더 예측 가능합니다 (p가 증가하면 상관 관계가 감소 함).
- 깊이 수준이 높을수록엘불균형을 계산하기 위해 고려되는 주문서의 불균형 측정치가 미래 가격 변동과 더 많이 연관 됨
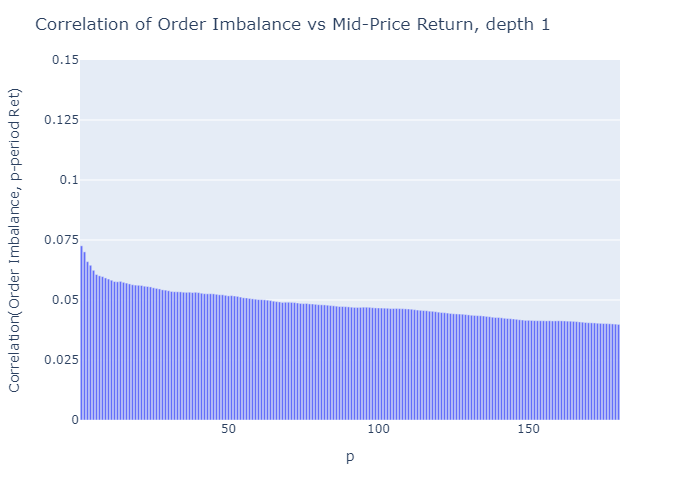
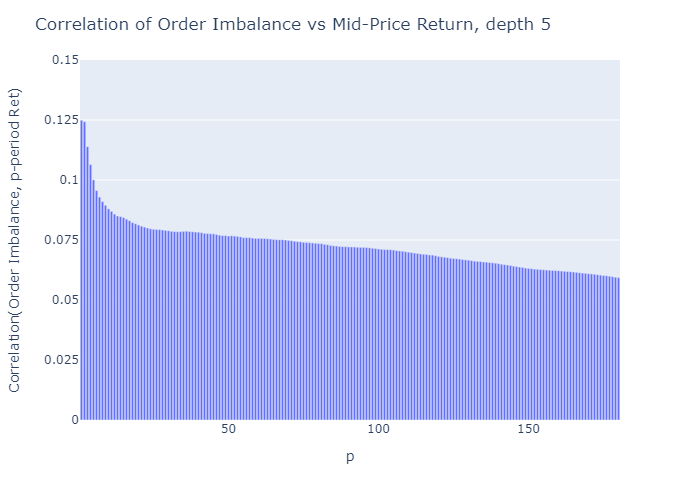
깊이에 대한 해당 플롯L = 2…에4간결하게 보여주지 않는 것은 이러한 결과와 일치합니다.이러한 플롯에 대한 Python 코드는 부록 A2를 참조하십시오.
가격 불확실성
위에 제시된 상관 관계는 불균형이 더 높은엘낮은 가격으로 계산 된 불균형보다 가격 상승과 더 나은 상관 관계엘.더 많은 단기 가격은 ρ와 더 높은 상관 관계를 갖습니다.이를 바탕으로 우리는 한 기간 앞선 예측 (≈10 초)만으로 분석을 계속합니다.
상관 관계는 평균 측정 값입니다. 중간 가격 움직임의 불확실성은 어떻습니까?
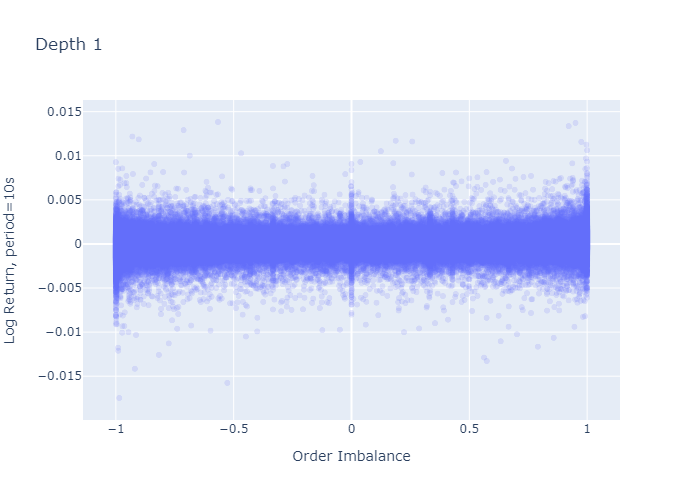
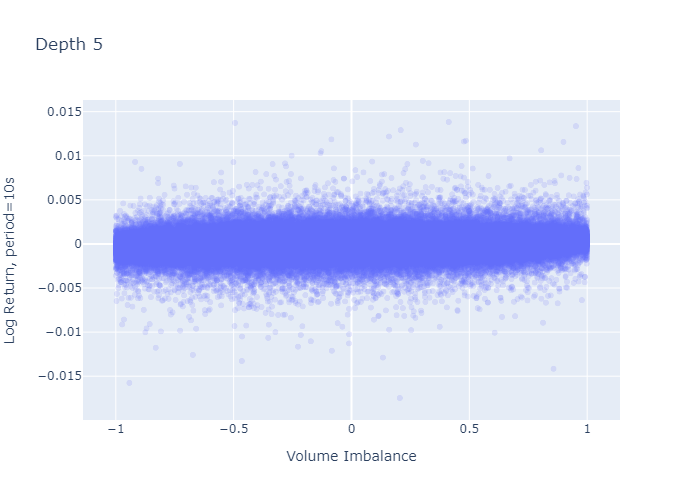
그림 7과 8은 기간 초에 관찰 된 불균형에 대한 1주기 로그 수익률을 보여줍니다.L = 1과L = 5각기.레벨 1 불균형 플롯 (그림 7)은 불균형이 크거나 (-1에 가까움 또는 1에 가까움) 0 일 때 로그 반환의 더 큰 변동이있는 것처럼 보이며, 이는 레벨 5 불균형에 대해 관찰되지 않습니다 (그림 8).그러나이 플롯의 더 큰 변동은 경계와 0 (그림 2 및 3의 히스토그램에서 볼 수 있음)에서 L = 1에 대해 더 많은 관측치를 가지고 있다는 사실에서 기인합니다. 수익률의 표준 편차를 계산해도 더 높은 것이 확인되지는 않습니다.다음 단락에서 볼 수 있듯이 극단에서의 차이.
불균형 체제
우리는 따른다Cartea et al.(2018)불균형 측정 값을 지점을 따라 균등하게 배치되도록 선택한 5 개 체제로 분류합니다.
θ = {-1, -0.6, -0.2, 0.2, 0.6, 1}.
즉, 정권 0은 -1과 -0.6 사이의 가격 불균형을 가지고 있고, 정권 1은 -0.6에서 -0.2까지 등등입니다.표 1은 5 개 체제 모두에 대한 1주기 선행 가격 수익률의 표준 편차를 보여줍니다.
표 1은 이전 단락의 질문을 다룹니다. 극심한 불균형 (정권 0 및 정권 4)에서 중간 가격 차이는 다음과 같습니다.아니주문 장 깊이 레벨 L = 1이 레벨 5보다 높습니다.
이제 우리는이 분석을 추가로 취하고 신뢰 구간을 구성하여 주어진 체제에서 예상되는 중간 가격 수익률에 대한 확률 적 한계를 추정합니다.이 계산에 대한 자세한 내용은 부록 A1에 나와 있습니다.
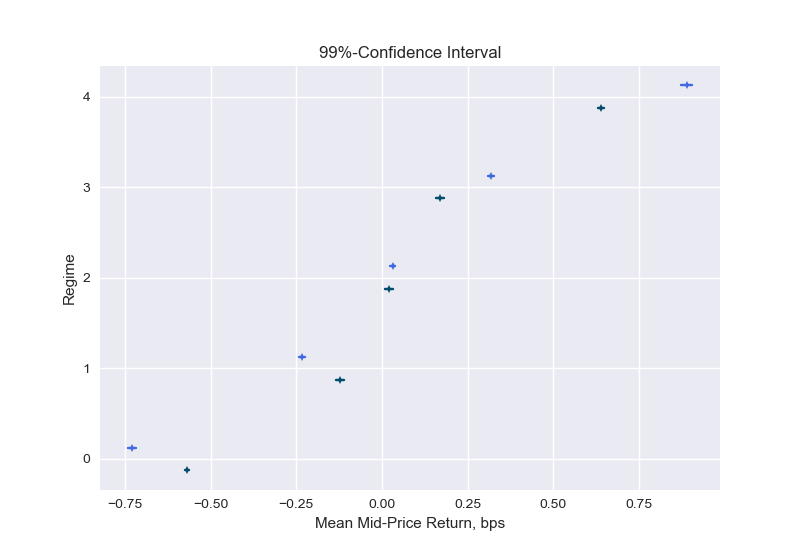
그림 9는 주어진 체제에서 예상되는 중간 가격 수익률에 대한 신뢰 구간을 보여줍니다.실제로 수익률은 낮은 불균형 수 (정권 0 및 1)에 대해 평균 음수이고 높은 불균형 수 (정규 3 및 4)에 대해 양수임을 알 수 있습니다.불균형이 더 높은 수준으로 구성 될 때 평균은 순서 불균형 방향으로 더 많이 이동합니다. 예를 들어, 영역 4에서 불균형이 다음과 같이 계산 될 때 1주기 선행 수익의 평균L = 1(진한 선)은 레벨의 깊이에서 계산을 수행 할 때보 다 작습니다.L = 5(밝은 선).표시된 신뢰 구간은 예상 값의 불확실성을 반영합니다.표 1의 표준 편차는이 예상 값 주변 수익률의 불확실성에 대해 알려줍니다.
이 분석은 상관 분석의 결과를 확인합니다. 불균형과 1주기 선행 수익 사이에는 양의 상관 관계가 있지만 약한 상관 관계가 있으며, 더 깊은 수준 (L)은 약간 더 예측 가능한 불균형 측정을 생성합니다.
경험적 확률
다음 기간 중간 가격이 우리가 어떤 불균형 체제에 속해 있는지 알면서 상승, 고정 또는 하락할 확률은 얼마입니까?
이를 확인하기 위해 모든 주문 불균형을 영역 0-4로 버킷 화 한 다음 음수 수익률, 0 수익률 및 양의 1 기간 수익률을 계산하고이 개수를 관측치 수로 나누어 확률에 대한 추정치를 구합니다.중간 가격 움직임.
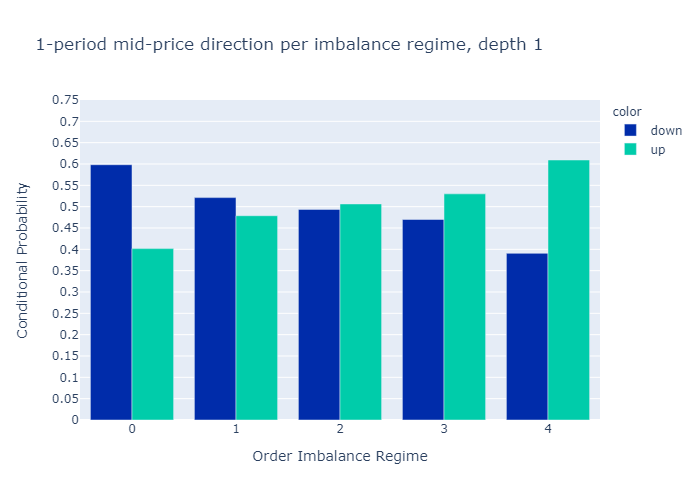
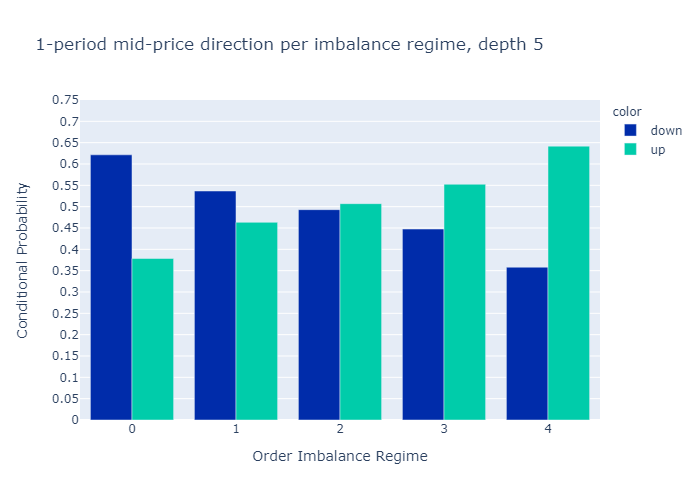
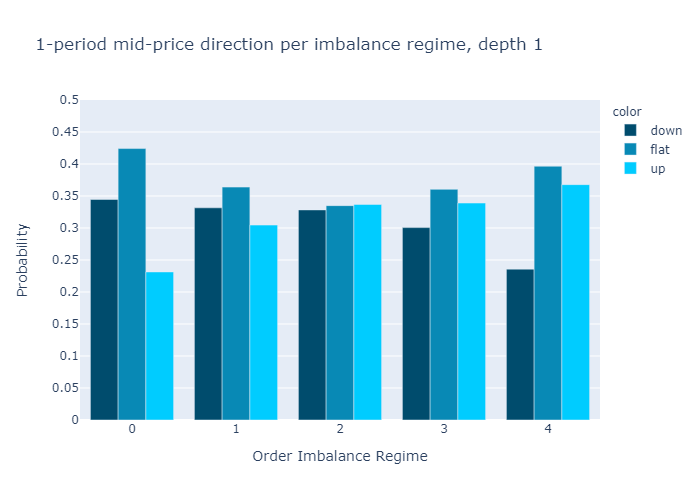
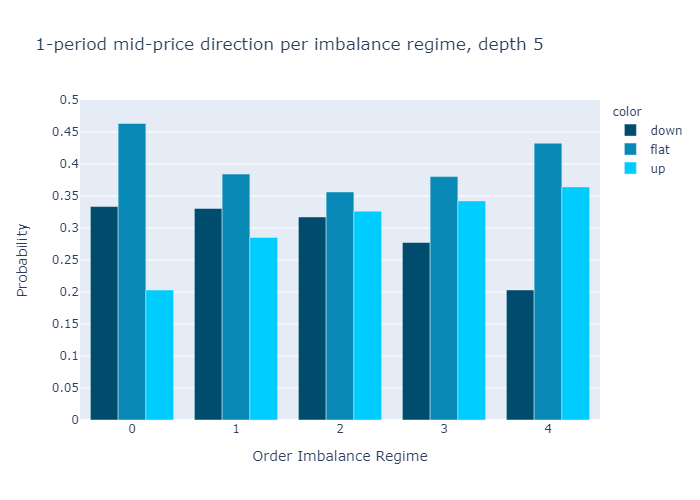
그림 10과 11은 다음에 대해 계산 된 불균형에 대한 경험적 확률을 보여줍니다.L = 1과L = 5각기.수치는 우리의 초기 가설을 확인합니다.
주문 장 불균형 값이 낮은 제도에서는 중간 가격이 하락할 가능성이 더 높으며 그 반대의 경우도 마찬가지입니다.
1 단계 (그림 10) 또는 5 단계 (그림 11)만으로 불균형을 계산할 때 경험적 확률에 질적으로 차이가 없음을 알 수 있습니다.우리는 더 높은 수준에 대한 확률이L = 5보다 차별적이다L = 1, 이는 원하는 속성입니다.
부록 A3에서 우리는 또한 0이 아닌 가격 변동을 관찰 할 때 조건부 확률을 보여줍니다.가격이 움직이면 레벨 5 불균형이 레벨 1 불균형보다 약간 더 나은 예측 변수입니다.
수익성

많은 암호 화폐 거래소에는 10bps의 거래 수수료가 있습니다 (그리고 우리는 2 번의 거래를 실행할 것입니다).신뢰 구간 (그림 9)에서 고려한 10 초 기간 동안 중간 가격 수익률이 10 베이시스 포인트 미만임을 알 수 있습니다.따라서 차이를 고려하지 않고 기대 수익률로 판단하면 주문 불균형이 매도-매도 스프레드를 조사하지 않고서도 자체적으로 수익성있는 전략을 의미하는 것은 아니라는 결론을 내릴 수 있습니다.
이 결과를 확인하기 위해 다른 각도에서 수익성을 살펴보고 그림 10 및 11과 유사하게 10 베이시스 포인트보다 큰 가격 변동의 경험적 확률을 계산합니다. 즉, 절대적으로 10 베이시스 포인트 미만인 모든 움직임을 다음과 같이 계산합니다.플랫.표 3은 주문 장 수준이 1과 5 모두 인 불균형 계산의 경우 대부분의 거래가 모든 체제에서 10 베이시스 포인트의 절대 수익 이하로 끝날 것임을 보여줍니다.이것은 전략이 자체적으로 통계적 차익 거래를 허용하지 않음을 확인합니다.
결론
ETHUSD 주문 장 및 중간 가격 움직임에 대한 우리의 분석은 주식 시장의 주문 장 불균형에 대한 문헌의 결과와 일치합니다.
- 불균형이 -1에 가까울 때 매도 압력이 있고 단기적으로 중가가 하락할 가능성이 더 높고, 불균형이 1에 가까울 때 매수 압력이 있고 중간 가격이이동.
- 불균형 조치의 가격 영향은 수명이 짧으며 시간이 지남에 따라 빠르게 악화됩니다.
- 불균형 측정 자체는 통계적 차익 거래에 직접 사용할 수 없지만 알고리즘을 개선하는 데 사용할 수 있습니다.
오더 북 불균형에 대한 문헌에서 인용 한 것 외에도 최대 5 개 레벨을 사용하여 계산 된 오더 북 불균형을 분석 한 결과 불균형 측정 값과 미래 가격 움직임과의 상관 관계가 레벨에 따라 증가한다는 것을 발견했습니다 (평가 된 5 개 레벨에 대해)..그러나 그림 9의 기대 값과 신뢰 구간에서 높은 수준은 수익 방향을 약간 개선 할 뿐이며, 더 높은 수준의 주문 장 깊이로 작업 할 때 경험적 확률이 약간 더 차별적이라는 것을 관찰했습니다.따라서, 더 깊은 레벨 (L & gt; 1)에서 추가 된 값은 아마도 더 높은 복잡성을 정당화하지 않을 것입니다 (더 깊은 레벨을 처리하는 것은 일반적으로 고주파 알고리즘에 대해 더 많은 시간이 소요됨).
마지막으로 불균형과 가격 변동 사이의 가장 강력한 관계가 데이터에서 사용할 수있는 가장 짧은 기간 (10 초) 내에 있음을 발견했습니다.따라서 틱 데이터를 살펴보면이 기사에서 살펴본 10 초의 기간과 달리 더 많은 통찰력을 얻을 수 있다고 결론지었습니다.
참고 문헌
Cartea, A., R. Donnelly 및 S. Jaimungal (2018).주문 장 신호로 거래 전략을 강화합니다.응용 수학 금융25 (1), 1-35.
Cartea, A., S. Jaimungal 및 J. Penalva (2015).알고리즘 및 고주파 거래.캠브리지 대학 출판부.
Cont, R., A. Kukanov 및 S. Stoikov (2014).오더 북 이벤트의 가격 영향.Journal of Financial Econometrics12 (1), 47-88.
Lipton, A., U. Pesavento 및 M.G. Sotiropoulos (2013).지정가 주문서의 무역 도착 역학 및 견적 불균형.arXiv 프리 프린트 arXiv : 1312.0514.
Paolella, MS (2007).중간 확률 : 계산적 접근.John Wiley & amp;자제.
Silantyev, E. (2018).암호 화폐 시장의 주문 흐름 분석.매질.
Stoikov, S. (2017).마이크로 가격 : 미래 가격에 대한 높은 빈도의 추정치.SSRN 2970694에서 사용 가능합니다.
부록
A1.신뢰 구간
우리는 주어진 체제에 있다는 조건으로 로그 반환의 평균에 관심이 있습니다.주어진 체제에서 예상되는 중간 가격 수익률에 대한 확률 적 한계를 추정 할 수있는 신뢰 구간을 구성합니다.여기에 제시된 방법은 표준입니다 (예 : Paollela 2017 참조).
에 의해중심 한계 정리, 표본 평균
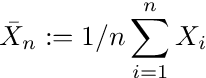
의i.i.d.랜덤 변수Xi정상입니다 :
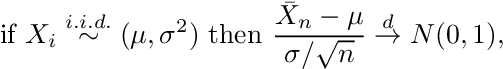
어디Xi대표하다i = 1,…, n평균이있는 분포에서 도출 된 관측치μ및 표준 편차σ, 위첨자가있는 화살표디분포 수렴을 나타내고 N (0,1)은 표준 정규 분포를 나타냅니다.방정식 A.2를 표현할 수 있습니다.비공식적으로
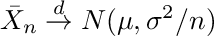
평균과 분산의 추정치로 이어지는
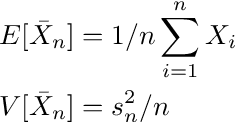
어디에스표본 표준 편차입니다.이제 수준 (1-α)에 대한 신뢰 구간은 다음과 같이 지정됩니다.
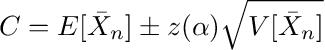
z (α)다음보다 큰 값을 관찰 할 확률이되도록 표준 정규 밀도 곡선의 x 축에있는 점을 나타냅니다.z (α)이하-z (α)α와 같습니다.
이 형태의 중앙 한계 정리를 적용하려면 중간 가격 수익률이i.i.d..중간 가격 수익률의 자기 상관은 1 % 미만이며 (A2 참조) 다른 분포에서 비롯되거나 상관 관계에 반영되지 않은 다른 종속성을 가져야한다는 표시가 없으므로 다음을 가정 할 수 있습니다.i.i.d.재산 보유 및 사용 방정식 A.4.
scipy.stats를 st로 가져 오기
numpy를 np로 가져 오기def Estimated_confidence (shifted_return,
vol_binned,
volume_regime_num,
alpha = 0.1) :
"" "
주어진 알파에 대한 신뢰 구간 추정
: paramshifted_return : 계산할 반환 배열
신뢰 구간
평균의 NaN 포함 가능
:유형shifted_return : 길이 n의 부동 소수점 배열
: paramvol_binned : 볼륨 체제.항목 i는
volume regime associated with
shifted_return[i]
:typevol_binned : 길이 n의 부동 배열
: param volume_regime_num: equals np.max(vol_binned)+1
:유형volume_regime_num : 정수
:반환: confidence intervals for mean of the returns per regime
: rtype: float array of size volume_regime_num x 2
"""
Confident_interval = np.zeros ((volume_regime_num, 2))
z = st.norm.ppf (1- 알파)
for regime_num in range(0, volume_regime_num):
m = np.nanmean (shifted_return [vol_binned == regime_num])
s = np.nanstd (shifted_return [vol_binned == regime_num])
sqrt_n = np.sqrt(np.sum(vol_binned == regime_num))
confidence_interval[regime_num, :] = [m - z * s/sqrt_n,
m + z * s / sqrt_n]
return confidence_interval
A2. Plot the autocorrelation function
아래의 Python 코드 조각은 자기 상관과 플롯을 계산합니다.계산은 11 초보다 큰 시계열의 (하드 코딩 된) 간격을 설명합니다.
numpy를 np로 가져 오기
datetime 가져 오기 datetime에서
import plotly.express as pxdef shift_array(v, num_shift):
'' '
배열을 왼쪽 (num_shift & lt; 0) 또는 오른쪽 num_shift & gt; 0으로 이동
: paramv : 이동할 float 배열
:유형v : 어레이 1d
: param num_shift: number of shifts
:typenum_shift : 정수
:반환: 원래 배열과 동일한 길이의 부동 배열,
num_shifts 요소로 이동, np.nan
경계의 항목
: rtype: array
'''
v_shift = np.roll (v, num_shift)
num_shift & gt;0 :
v_shift [: num_shift] = np.nan
그밖에:
v_shift [num_shift :] = np.nan
반환 v_shiftdef plot_acf(v, max_lag, timestamp):
'' '
자기 상관 함수를 플로팅하기위한 Figure 생성
:parammax_lag : 자기 상관을 중지 할시기
계산 (최대 max_lag 시차까지)
: param timestamp: timestamp array of length n
with entry i corresponding to timestamp of
entry i in v, used to remove time-jumps
v : n 개의 관측치가있는 배열
:return: 음모 그림
'' '
corr_vec = np.zeros (max_lag, dtype = float)
for k in range(max_lag):
v_lag = shift_array (v, -k-1)
timestamp_lag = shift_array (타임 스탬프, -k-1)
dT = (timestamp - timestamp_lag) / (k+1)
msk_time_gap = dT & gt;11000.0
마스크 = ~ np.isnan (v) & amp;~ np.isnan (v_lag) & amp;~ msk_time_gap
corr_vec [k] = np.corrcoef (v [마스크], v_lag [마스크]) [0, 1]
fig_acf = px.bar (x = 범위 (1, max_lag + 1), y = corr_vec)
fig_acf.update_layout (yaxis_range = [0, 1])
fig_acf.update_xaxes (title = "Lag")
fig_acf.update_yaxes(title="ACF")
return fig_acf
A3. Conditional Empirical Probabilities
그림 A1과 A2는 0이 아닌 수익률을 관찰 할 때 중간 가격 상승 / 하강 이동의 경험적 확률을 보여줍니다.수준 5 불균형은 더 나은 차별 력을 보여줍니다. 즉, 영역 0과 5에서 확률은 수준 1보다 더 극단적입니다.
If the mid-price moves, the imbalance with L=5 is a better indicator of the price direction than the imbalance of L=1.